Program
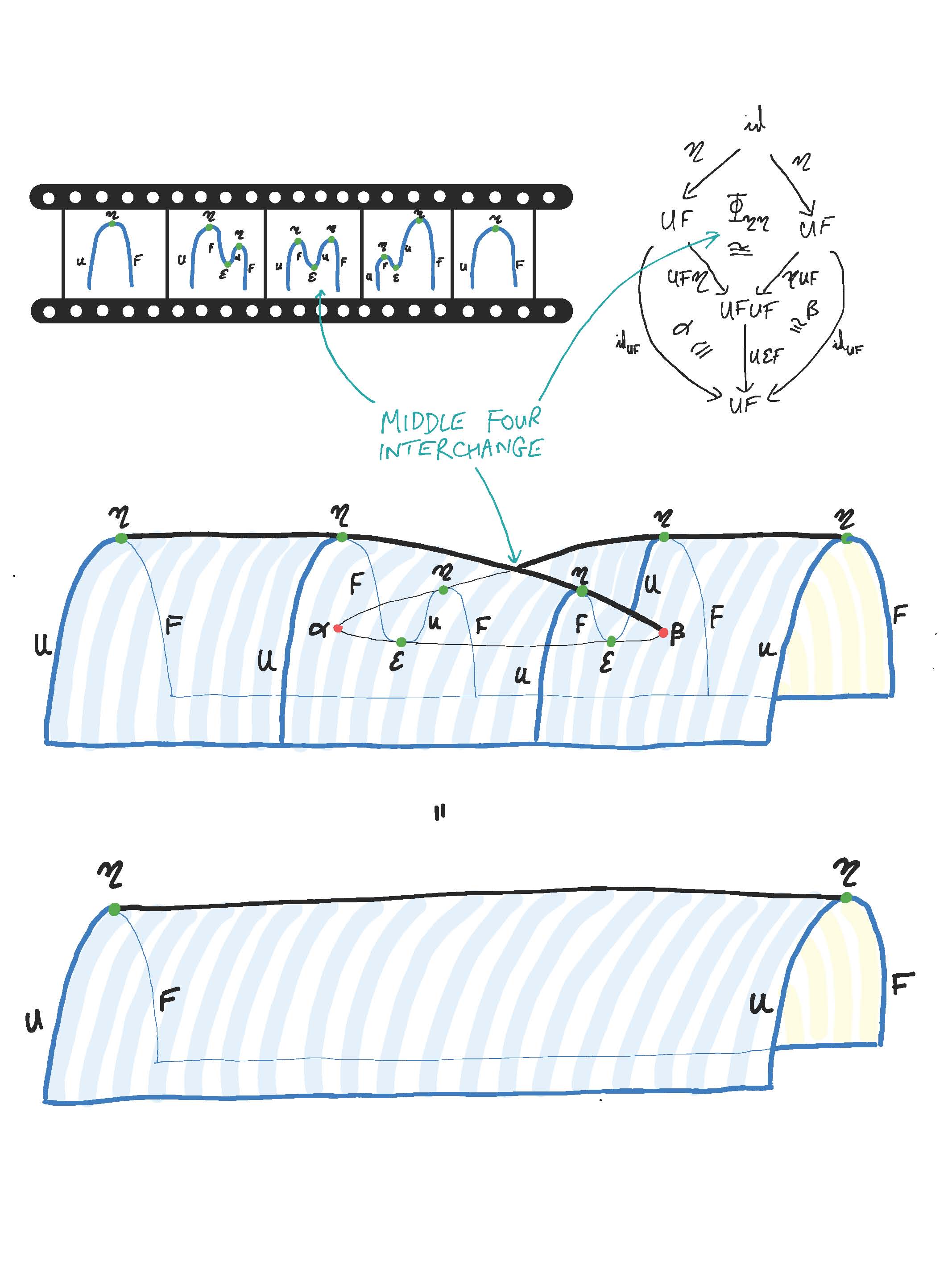
swallowtail identity
Though many of the ideas in higher category theory find their origins in homotopy theory — for instance as expressed by Grothendieck’s “homotopy hypothesis” — the subject today interacts with a broad spectrum of areas of mathematical research. Unforeseen descent, or local-to-global formulas, for familiar objects can be articulated in terms of higher invertible morphisms. Compatible associative deformations of a sequence of maps of spaces, or derived schemes, can putatively be represented by higher categories, as Koszul duality for E_n-algebras suggests. Higher categories offer unforeseen characterizing universal properties for familiar constructions such as K-theory. Manifold theory is natively connected to higher category theory and adjunction data, a connection that is most famously articulated by the recently proven Cobordism Hypothesis.
In parallel, the idea of "categorification'' is playing an increasing role in algebraic geometry, representation theory, mathematical physics, and manifold theory, and higher categorical structures also appear in the very foundations of mathematics in the form of univalent foundations and homotopy type theory. A central mission of this semester will be to mitigate the exorbitantly high "cost of admission'' for mathematicians in other areas of research who aim to apply higher categorical technology and to create opportunities for potent collaborations between mathematicians from these different fields and experts from within higher category theory.
Bibliography
Program Photography
Keywords and Mathematics Subject Classification (MSC)
Tags/Keywords
higher categories
categorification
infinity-categories
algebraic K-theory
Factorization homology
cobordism hypothesis
synthetic higher categories
Grothendieck-Teichmuller
infinity-operads
topological quantum field theory
Mackey functors
19Fxx - $K$K-theory in number theory [See also 11R70, 11S70]
55Pxx - Homotopy theory {For simple homotopy type, see 57Q10}
55Uxx - Applied homological algebra and category theory in algebraic topology [See also 18Gxx]
57Txx - Homology and homotopy of topological groups and related structures
81Txx - Quantum field theory; related classical field theories [See also 70Sxx]
