Summer Graduate School

Several executions of a 3-dimensional sumcheck protocol with a random order of directions (thanks to Dev Ojha for creating the diagram)

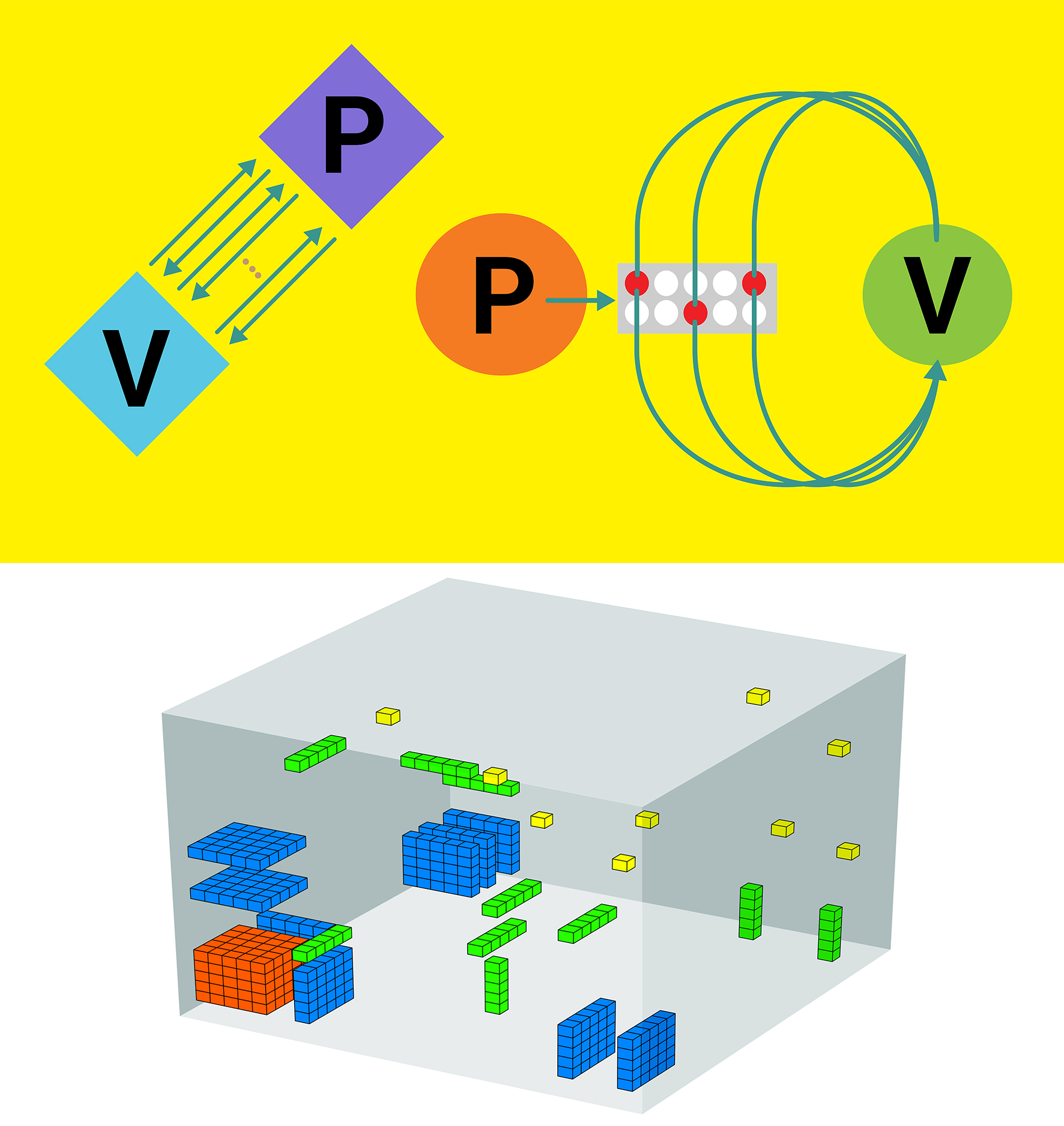
Proofs are at the foundations of mathematics. Viewed through the lens of theoretical computer science, verifying the correctness of a mathematical proof is a fundamental computational task. Indeed, the P versus NP problem, which deals precisely with the complexity of proof verification, is one of the most important open problems in all of mathematics.

The complexity-theoretic study of proof verification has led to exciting reenvisionings of mathematical proofs. For example, probabilistically checkable proofs (PCPs) admit local-to-global structure that allows verifying a proof by reading only a minuscule portion of it. As another example, interactive proofs allow for verification via a conversation between a prover and a verifier, instead of the traditional static sequence of logical statements. The study of such proof systems has drawn upon deep mathematical tools to derive numerous applications to the theory of computation and beyond.

In recent years, such probabilistic proofs received much attention due to a new motivation, delegation of computation, which is the emphasis of this summer school. This paradigm admits ultra-fast protocols that allow one party to check the correctness of the computation performed by another, untrusted, party. These protocols have even been realized within recently-deployed technology, for example, as part of cryptographic constructions known as succinct non-interactive arguments of knowledge (SNARKs).

This summer school will provide an introduction to the field of probabilistic proofs and the beautiful mathematics behind it, as well as prepare students for conducting cutting-edge research in this area.

Courses. The summer graduate school will start with two days of introductory material for everyone, covering definitions and simple examples of interactive proofs and probabilistically checkable proofs. Subsequently, two complementary courses will be offered:

• A foundations course, covering the "classics" of probabilistic proofs. The material includes seminal results that have found a diverse set of applications in theoretical computer science.
• A frontiers course, covering contemporary results in probabilistic proofs. The focus of this course is on proof protocols for delegating computations.

Students are encouraged to attend both courses, which have comparable difficulty and are designed to complement each other.

Suggested prerequisites

(1) Fundamentals of computational complexity.
For example, chapters 1,2,4,6,7 of Computational Complexity: A Modern Approach by Sanjeev Arora and Boaz Barak. Most importantly:

• Turing machines, complexity classes, and reductions (1.2-1.5, 2.2).
• The Cook-Levin theorem (2.3).
• Familiarity with the classes P, NP, PSPACE, NEXP, and their complete languages (1.6, 2.1, 2.6, 4.1, 4.2).
• The computation model of Boolean circuits, circuit satisfiability, and exponential size circuits (6.1-6.4, 6.8).
• Probabilistic computation and the class BPP (7.1-7.4).

(2) Basic knowledge of finite fields and their properties.
For example, as covered in the following references:

• David Forney's Introduction to finite fields (chapter 7).
• A. Sutherland's notes on finite fields and integer arithmetic.
• V. Guruswami's cheat sheet on finite fields.

Bibliography

For eligibility and how to apply, see the Summer Graduate Schools homepage

Due to the small number of students supported by MSRI, only one student per institution will be funded by MSRI.