Summer Graduate School
| Parent Program: | -- |
|---|---|
| Location: | Center for Mathematics of University of Notre Dame |
Show List of Lecturers
- Mark Johnson (University of Arkansas)
- Linquan Ma (Purdue University)
- Claudia Polini (University of Notre Dame)
- Javid Validashti (DePaul University)
Show List of Speakers
- Robin Hartshorne
- Uwe Nagel (University of Kentucky)
This summer school is held at the University of Notre Dame. Here is where one can find additonal information about the summer school, https://www3.nd.edu/~cmnd/programs/cmnd2019/graduate/index.html.
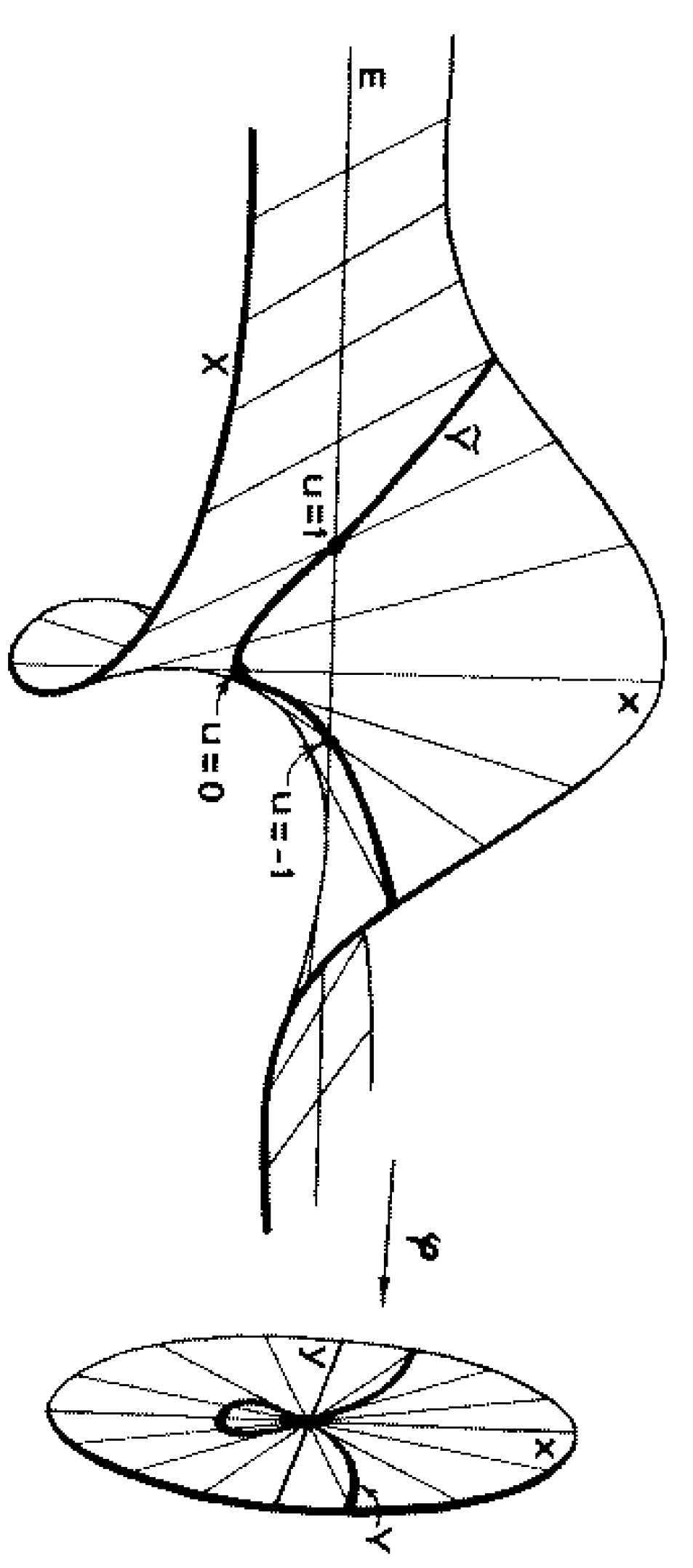
Linkage is a method for classifying ideals in local rings. Residual intersections is a generalization of linkage to the case where the two `linked' ideals need not have the same codimension. Residual intersections are ubiquitous: they play an important role in the study of blowups, branch and multiple point loci, secant varieties, and Gauss images; they appear naturally in intersection theory; and they have close connections with integral closures of ideals.
Commutative algebraists have long used the Frobenius or p-th power map to study commutative rings containing a finite fi eld. The theory of tight closure and test ideals has widespread applications to the study of symbolic powers and to Briancon-Skoda type theorems for equi-characteristic rings.
Numerical conditions for the integral dependence of ideals and modules have a wealth of applications, not the least of which is in equisingularity theory. There is a long history of generalized criteria for integral dependence of ideals and modules based on variants of the Hilbert-Samuel and the Buchsbaum-Rim multiplicity that still require some remnants of finite length assumptions.
The Rees ring and the special fiber ring of an ideal arise in the process of blowing up a variety along a subvariety. Rees rings and special fiber rings also describe, respectively, the graphs and the images of rational maps between projective spaces. A difficult open problem in commutative algebra, algebraic geometry, elimination theory, and geometric modeling is to determine explicitly the equations defining graphs and images of rational maps.
The school will consist of the following four courses with exercise sessions plus a Macaulay2 workshop
- Linkage and residual intersections
- Characteristic p methods and applications
- Blowup algebras
- Multiplicity theory
Suggested prerequisites:
- An introduction to Commutative Algebra by Atiyah and MacDonald
- Commutative Algebra with a view towards algebraic geometry by David Eisenbud - Chapters 2-13 and 17-21
For eligibility and how to apply, see the Summer Graduate Schools homepage
Due to the small number of students supported by MSRI, only one student per institution will be funded by MSRI.
Linkage
residual intersections
multiplicities
Hilbert functions
Rees algebras
associated graded rings
tight closure
integral closure
symbolic powers
reductions
resolutions
Gorenstein rings
Cohen-Macaulay rings
canonical modules
local cohomology
Frobenious map
7 F-signature
Hilbert multiplicity
Hilbert-Kunz multiplicity
strongly F-regular rings
etale fundamental group
13A30 - Associated graded rings of ideals (Rees ring, form ring), analytic spread and related topics
13B21 - Integral dependence in commutative rings; going up, going down
13C05 - Structure, classification theorems for modules and ideals in commutative rings
13C40 - Linkage, complete intersections and determinantal ideals [See also 14M06, 14M10, 14M12]
13D02 - Syzygies, resolutions, complexes and commutative rings
13D22 - Homological conjectures (intersection theorems) in commutative ring theory
13D40 - Hilbert-Samuel and Hilbert-Kunz functions; Poincaré series
13D45 - Local cohomology and commutative rings [See also 14B15]
13H10 - Special types (Cohen-Macaulay, Gorenstein, Buchsbaum, etc.) [See also 14M05]
13H15 - Multiplicity theory and related topics [See also 14C17]
|
Jun 03, 2019 Monday |
|||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Jun 04, 2019 Tuesday |
|||||||||||||||||||||||||||||||||||||
|
Jun 05, 2019 Wednesday |
|||||||||||||||||||||||||||||||||||||
|
Jun 06, 2019 Thursday |
|||||||||||||||||||||||||||||||||||||
|
Jun 07, 2019 Friday |
|
||||||||||||||||||||||||||||||||||||
|
Jun 10, 2019 Monday |
|||||||||||||||||||||||||||||||||||||
|
Jun 11, 2019 Tuesday |
|||||||||||||||||||||||||||||||||||||
|
Jun 12, 2019 Wednesday |
|||||||||||||||||||||||||||||||||||||
|
Jun 13, 2019 Thursday |
|||||||||||||||||||||||||||||||||||||
|
Jun 14, 2019 Friday |
|