Summer Graduate School

<p>The discriminant ∆ detects singular varieties. The picture shows three different scenarios: solutions of quadratic polynomials, cubic plane curves and cubic surfaces.</p>

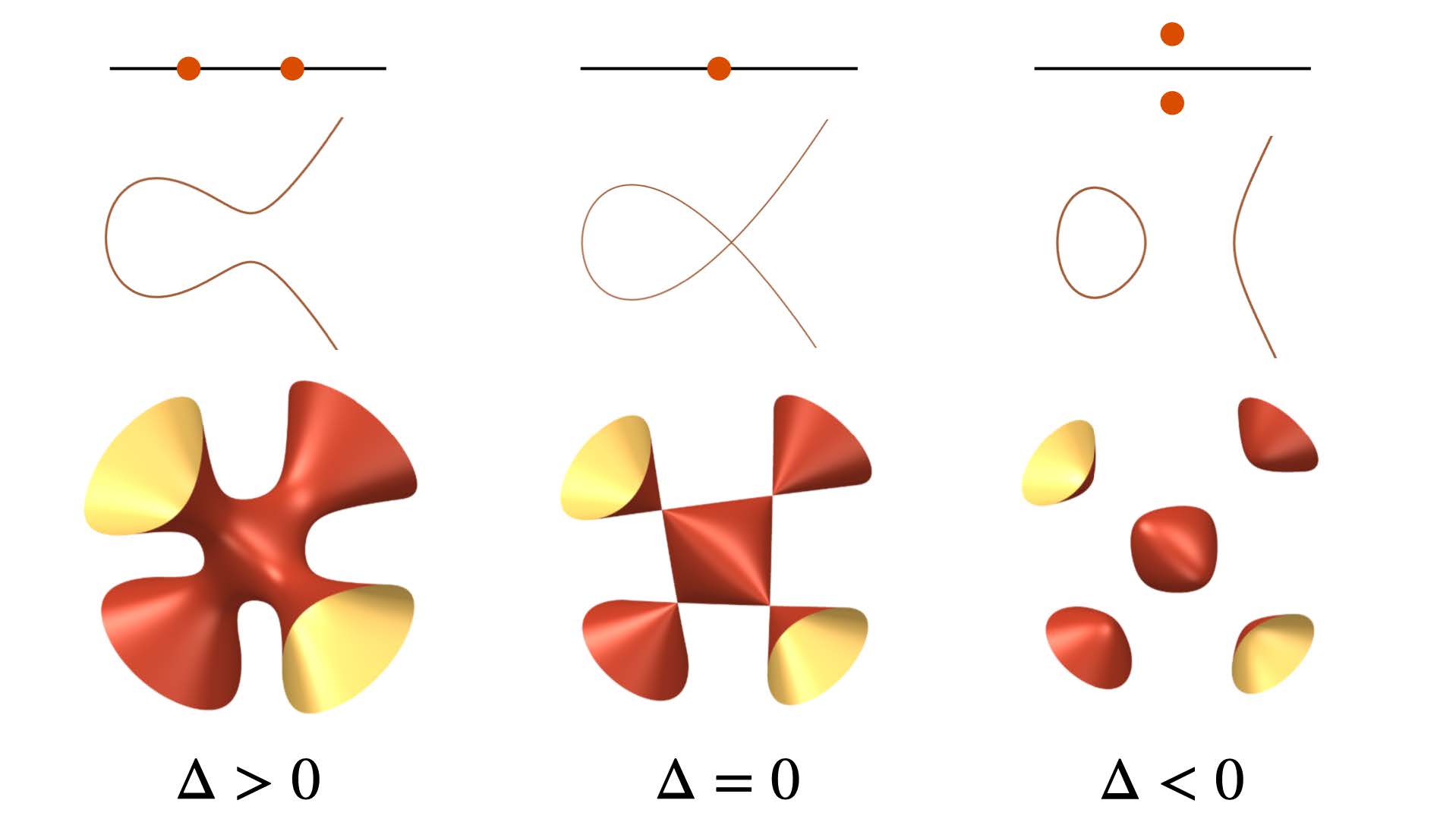
This summer school will offer a hands-on introduction to discriminants, with a view towards modern applications. Starting from the basics of computational algebraic geometry and toric geometry, the school will gently introduce participants to the foundations of discriminants. A particular emphasis will be put on computing discriminants of polynomial systems using computer algebra software. Then, we will dive into three applications of discriminants: algebraic statistics, geometric modeling, and particle physics. Here, discriminants contribute to the study of maximum likelihood estimation, to finding practical parametrizations of geometric objects, and to computations of scattering amplitudes. We will explain recently discovered unexpected connections between these three applications. In addition to lectures, the summer school will have daily collaborative exercise sessions which will be guided by the teaching assistants and will include software demonstrations.

School Structure

The school will be comprised of two lectures and two exercise sessions each day. 

The full schedule can be found HERE.

Prerequisites

Participants are expected to have a firm background in linear algebra and basic abstract algebra (e.g., commutative rings and their ideals). Familiarity with computational algebra at the level of the undergraduate textbook [9], chapters 1-4 and 8 is a plus. However, we will provide a concise review at the beginning of the workshop. Participants are expected to bring their laptop, with a computer algebra software system installed (e.g., Macaulay2, Maple, Oscar, Singular, . . . ). In preparation for the school, we encourage students to try out basic commands in such a computer algebra system which implement the algorithms introduced in the aforementioned chapters of [9]. Excellent resources for this are the exercises in [9, Chapter 2, §8] and the material from the Macaulay2 Bootcamp held in Leipzig in 2022 which is available at https://mathrepo.info/M2_bootcamp/index.html. Basic knowledge of toric varieties (e.g., chapters 1 and 2 of [10] or sections 2 and 3 of [26]) is helpful but not necessary. We will introduce our application areas from scratch: no background in algebraic statistics, geometric modeling or physics is required. 

References

[9] David A. Cox, John B. Little, and Donal O’Shea, Ideals, varieties, and algorithms, fourth ed., Undergraduate Texts in Mathematics, Springer, Cham, 2015, An introduction to computational algebraic geometry and commutative algebra. MR 3330490

[10] David A. Cox, John B. Little, and Henry K. Schenck, Toric varieties, Graduate Studies in Mathematics, vol. 124, American Mathematical Society, Providence, RI, 2011. MR 2810322

[26] Simon Telen, Introduction to toric geometry, arXiv:2203.01690 (2022)

Application Procedure

SLMath is only able to support a limited number of students to attend this school.  Therefore, it is likely that only one student per institution will be funded by SLMath.

For eligibility and how to apply, see the Summer Graduate Schools homepage.

Venue

The summer school will take place at the Max Planck Institute for Mathematics in the Sciences in Leipzig, Germany.  Students will be housed in nearby hotels.