Summer Graduate School

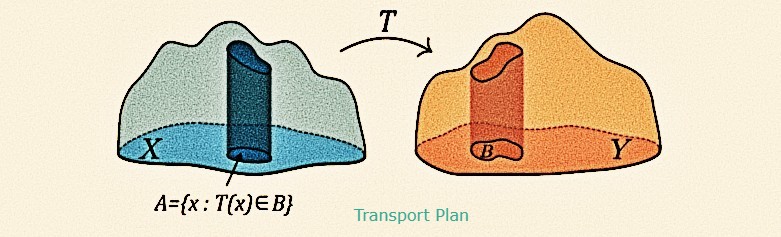
This summer school offers an exceptional opportunity for participants to delve into the intricate realm of statistical optimal transport theory. This captivating field stands at the crossroads of multiple disciplines, drawing from a rich tapestry of mathematical insights from diverse subjects, including partial differential equations, stochastic analysis, convex geometry, statistics, and machine learning, crafting a vibrant and interdisciplinary landscape. The foremost objective of this summer school is to create a dynamic learning environment that unites students from diverse backgrounds such as PDE theory, probability, or optimal transport. Throughout the program, participants will embark on a journey that will not only enhance their comprehension of the distinct elements of statistical optimal transport but will also foster the integration of diverse disciplines. This integration will enable them to tackle the forefront challenges in statistics and machine learning where optimal transport stands as a potent and indispensable tool. By the end of the program, participants will leave with not only a comprehensive skill set but also a profound understanding of the synergy between optimal transport and the realm of statistics and machine learning, ready to apply their knowledge to the forefront of this exciting field.

School Structure

There will be two lectures each day, as well as one or two problem sessions. 

Prerequisites

A foundational understanding of real analysis, encompassing basic measure theory [Dur10, Chapter 1], and a grasp of probability theory [Dur10, Chapter 2, 3] will be prerequisites for this course. Familiarity with concepts in convex analysis, including convexity, duality, [Roc70, Part 1, Basic Concepts, and Part 3, Duality Correspondences] and fundamental principles in convex optimization, will be highly advantageous. While some exposure to PDE theory could prove beneficial, it is not mandatory. This background is considered ideal, but it’s not an absolute requirement. We acknowledge that participants will have diverse knowledge and abilities, so we are committed to ensuring everyone reaches a common foundation. In the weeks leading up to the school, we will provide recommended readings to assist participants in better preparing for the course.

[Dur10] R. Durrett. Probability: theory and examples, volume 31 of Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press, Cambridge, fourth edition, 2010, or fifth edition, 2019 (alternate).

[Roc70] R. T. Rockafellar. Convex analysis (EZproxy), volume No. 28 of Princeton Mathematical Series. Princeton University Press, Princeton, NJ, 1970.

Recommended Preparatory Reading

Application Procedure

For eligibility and how to apply, see the Summer Graduate Schools homepage.