Summer Graduate School

<p>A wall-crossing in a moduli problem</p>

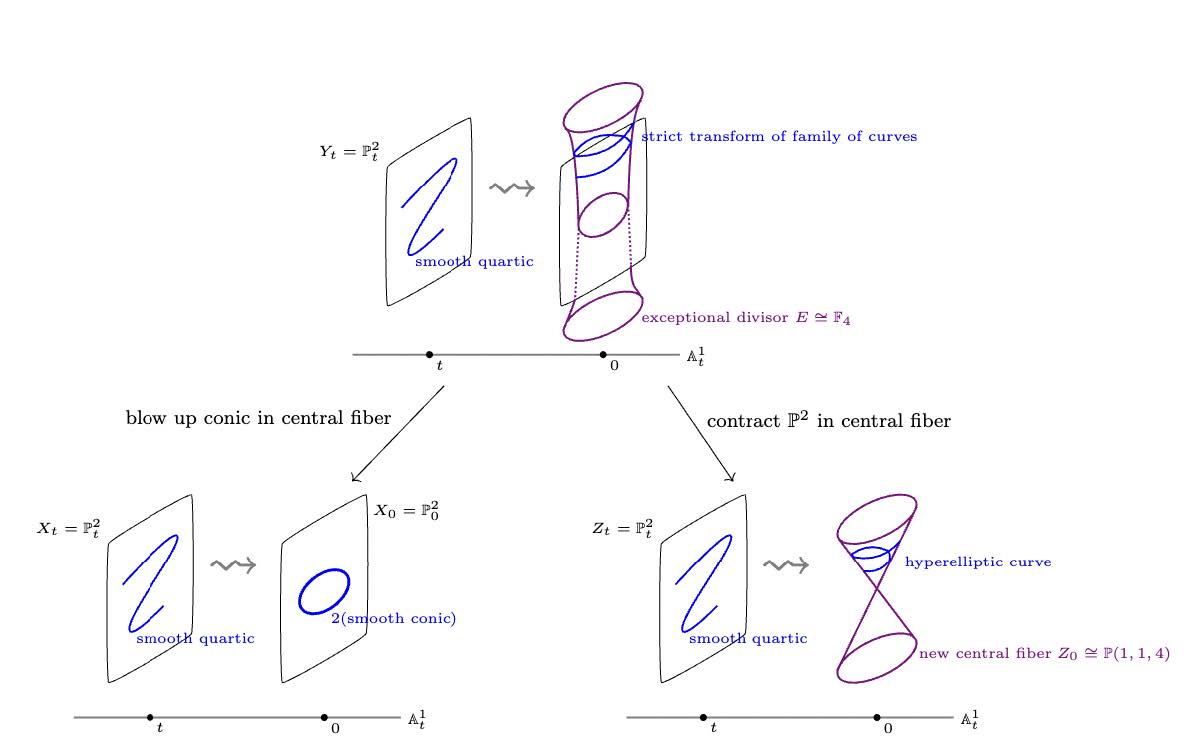
One of the central problems in algebraic geometry is to classify so-called algebraic varieties: geometric shapes cut out by polynomial equations. Algebraic varieties are parametrized by certain moduli spaces (roughly: parameter spaces whose points correspond to these different varieties). The geometry of these moduli spaces encodes the ways of continuously deforming these shapes. Furthermore, classification questions for algebraic varieties often boil down to understanding the geometry of these moduli spaces. In the past few years, powerful new tools have been developed in moduli theory, especially for higher dimensional varieties – those which are of complex dimension at least two. The goal of this summer school is to provide an introduction to many of these recently emerging breakthroughs to enable graduate students to begin working in this area. The program will be motivated and often guided by examples and is intended to be accessible to a wide variety of students.

With this in mind, we expect that students will gain an understanding of:

• higher dimensional algebraic geometry through the lens of birational geometry and the minimal model program,
• moduli spaces of varieties of general type (KSBA moduli),
• moduli of Fano varieties (K-moduli),
• standard tools for constructing and studying moduli spaces, such as Geometric Invariant Theory (GIT), stacks and their coarse/good moduli spaces, wall-crossing techniques, etc.
• specific examples of moduli spaces, e.g. genus g curves and K3 surfaces.

Students will also have the opportunity to work through examples, and read through many recent papers and preprints in this field.

School Structure

There will be two lectures each day, each followed by an accompanying problem sessions.

Prerequisites

This summer graduate school is aimed towards students who have completed a standard one year introductory course in foundational algebraic geometry, or who have read through (the equivalent of) the first three chapters of Hartshorne’s "Algebraic Geometry" (especially chapters II and III: scheme theory and cohomology). The problems in the chapter(section)s I(1-2), II(1-8), III(2-5) and III(9) are especially relevant to the subject. An alternative reference is (the much longer) Vakil’s "Foundations of Algebraic Geometry" (prepublication PDF), especially chapters 2, 3, 4, 11, 16, 21, 24.

Application Procedure

For eligibility and how to apply, see the Summer Graduate Schools homepage.