Workshop

Zoom Link

Investigating mixtures of bosons and fermions is an extremely active area of research in experimental physics for constructing and understanding novel quantum bound states such as those in superconductors, superfluids, and supersolids. These ultra-cold Bose-Fermi mixtures are intrinisically different from gases with only bosons or fermions. Namely, they show a fundamental instability due to energetic considerations coming from the Pauli exclusion principle. Inspired by this activity in the physics community, recently we started exploring the mathematical theory of Bose-Fermi mixtures. 

• One of the main challenges is understanding the physical scales of the system that allow for suitable analysis.  We will describe how we overcame this challenge in the joint work with Esteban Cárdenas and Joseph Miller by identifying a novel scaling regime in which the fermion distribution behaves semi-clasically, but the boson field remains quantum-mechanical. In this regime, the bosons are much lighter and more numerous than the fermions. 
• Time permitting, we will also describe new results obtained with Esteban Cárdenas, Joseph Miller and David Mitrouskas inspired by recent experiments by DeSalvo et al.  on mixtures of light fermionic atoms and heavy bosonic atoms. A key observation - and this has been theoretically long predicted - is the emergence of an attractive fermion-mediated interaction between the bosons. We give a rigorous derivation of fermion-mediated interactions and prove the associated stability-instability transition.

 Zoom Link

Zoom Link

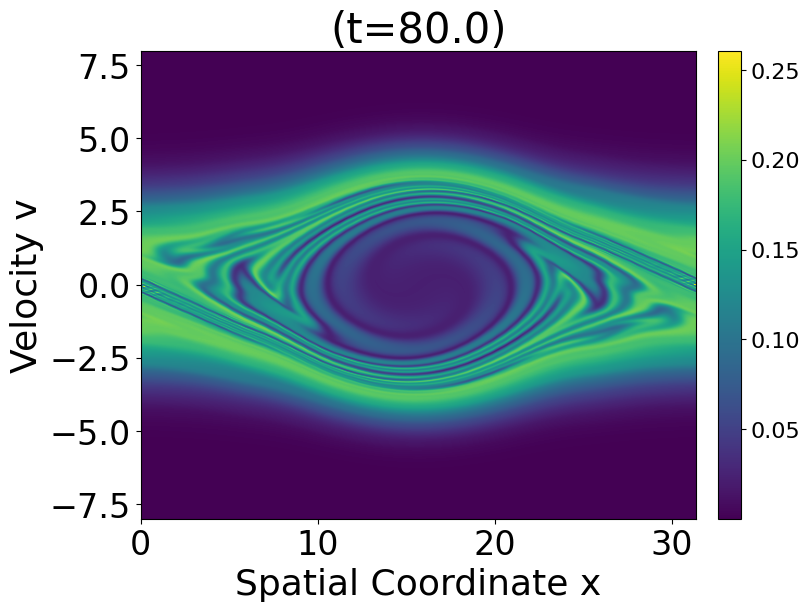
The talk briefly reviews Landau damping and plasma oscillations, as well as progress on their mathematical justification, that arise due to long-range interaction of particles modeled through the meanfield models such as the Hartree and Vlasov theory.

Zoom Link

We present recent developments in the mathematical study of the stochastic Gross–Pitaevskii equation, focusing on the well-posedness.

Zoom Link

The Vlasov-Maxwell-Landau equation is widely regarded as a first-principles model for plasma physics. In this talk, we introduce a novel particle method for this equation that simultaneously models particle transport, electromagnetic field effects, and Coulomb collisions. The method arises from a regularization of the variational formulation of the Landau collision operator, leading to a discretization that conserves mass, momentum, and energy, while also dissipating entropy. We will also discuss recent progress on energy-conserving time discretizations applied to the resulting particle system.