Summer Graduate School

Image by Nick Schmitt

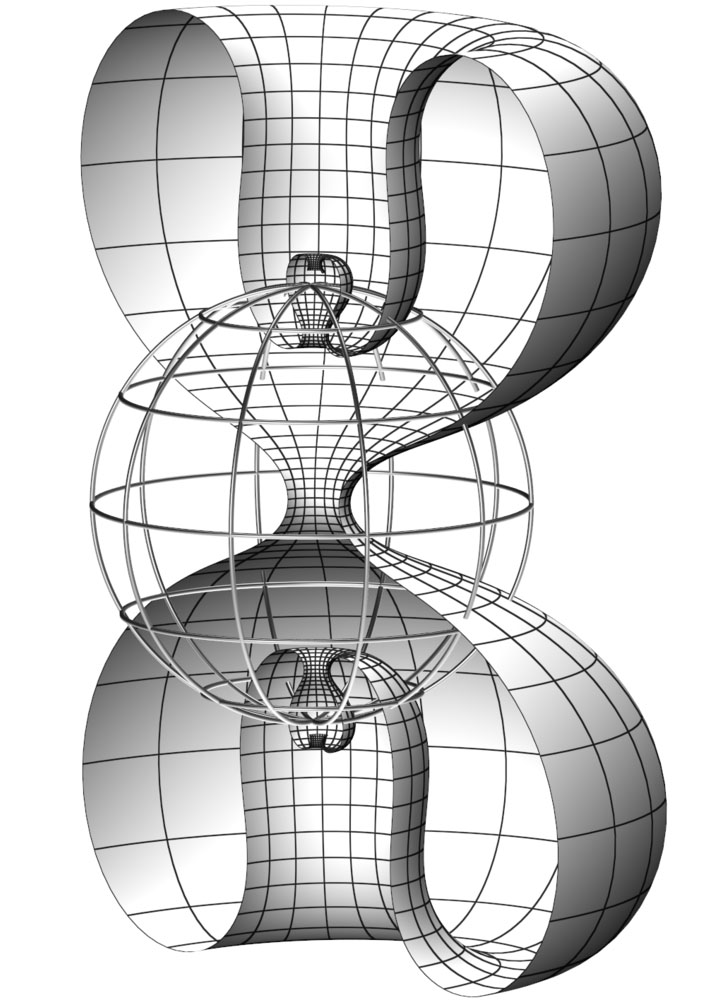
Figure 1. A rotationally symmetric solution to the self-duality equations on an open and dense subset of the torus. Singularities appear where the surface intersects the ideal boundary at infinity of the hyperbolic 3-space visualized by the wireframe.

Gauge theory is a geometric language used to formulate many fundamental physical phenomena, which has also had profound impact on our understanding of topology. The main idea is to study the space of solutions to partial differential equations admitting a very large group of local symmetries. Starting in the late 1970s, mathematicians began to unravel surprising connections between gauge theory and many aspects of geometric analysis, algebraic geometry and low-dimensional topology. This influence of gauge theory in geometry and topology is pervasive nowadays, and new developments continue to emerge.

The goal of the summer school is to introduce students to the foundational aspects of gauge theory, and explore their relations to geometric analysis and low-dimensional topology. By the end of the two-week program, the students will understand the relevant analytic and geometric aspects of several partial differential equations of current interest (including the Yang-Mills ASD equations, the Seiberg-Witten equations, and the Hitchin equations) and some of their most impactful applications to problems in geometry and topology.

School Structure

After introductory lectures for the first two days, we will proceed with the minicourse on Seiberg-Witten equations and the topology of to 4-manifolds in the mornings, and the the minicourse on Yang-Mills equations and harmonic maps in the afternoons. While the lectures will focus on introducing the main concepts and ideas, we expect the students to work on key concrete examples during the collaborative problems sessions. Lecturers will design the list of problems. The sessions will be supervised by the Lecturers and Teaching Assistants. At the end of each session students will be asked to present solutions to the problems assigned. This will allow us to gauge directly the engagement and understanding of the students, and get helpful feedback for the following lectures.

Suggested Prerequisites

We ask the graduate student participants to study the following topics either in course work or self-study in advance in order to arrive at the summer school well prepared. The essential material regarding the last three topics will be reviewed in the first few lectures of the summer school.

Differential Topology: Smooth manifolds, transversality, and Lie groups. References for these topics include:

• Guillemin-Pollack, Differential Topology (Chapters 1-2)

• Milnor, Topology from the Differentiable Viewpoint (Chapters 1-2)

• Warner, Foundations of Differentiable Manifolds and Lie Groups (Chapters 1-4).

Algebraic topology: Singular and CW Homology.

• Hatcher, Algebraic Topology (Chapters 2,3).

Functional analysis:

• Donaldson-Kronheimer, The geometry of four-manifolds (Appendix).

• Evans, Partial Differential Equations (Appendix B).

Riemannian geometry and bundles:

• Roe, Elliptic operators, topology and asymptotic methods (Chapters 1-2).

Riemann surfaces:

• Donaldson, Riemann surfaces (Chapters 1-4).

For eligibility and how to apply, see the Summer Graduate Schools homepage