Summer Graduate School

<p>A plane partition and an hourglass plabic graph</p>

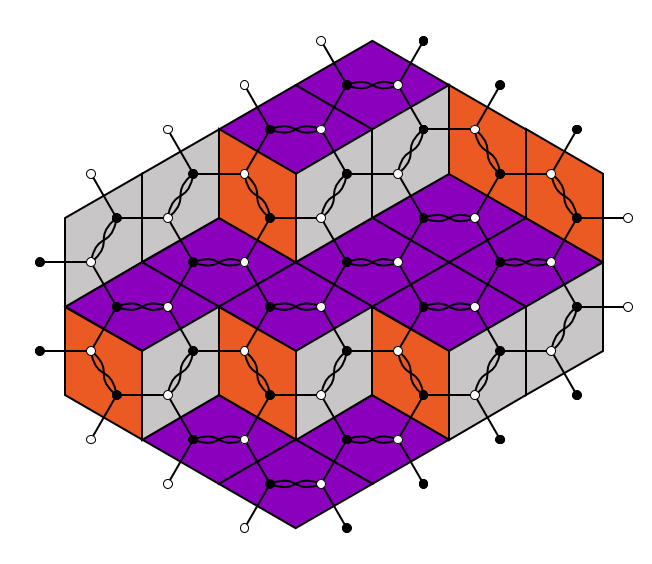
This school will introduce students to a range of powerful combinatorial tools used to understand algebraic objects ranging from the homogeneous coordinate ring of the Grassmannian to symmetric functions.   The summer school will center around two main lecture series "Webs and Plabic Graphs" and "Vertex Models and Applications".   While the exact applications differ, both courses will center on graphical models for algebraic problems closely related to Grassmannian and its generalizations.  This school will be accessible to a wide range of students.  Students will leave the school with a solid grasp of the combinatorics of webs, plabic graphs, and the six-vertex model, an understanding of their algebraic applications, and a taste of current research directions.

School Structure

There will be two lectures each day, as well as two problem sessions. 

Prerequisites

(1) Abstract Algebra by Dummit and Foote, 3rd edition

(a) Chapter 1, Introduction to Groups 
(b) Section 4.1, Group Actions and Permutation Representations 
(c) Sections 7.1-7.4, Introduction to Rings 
(d) Chapter 11, Vector Spaces 

(2) Section 2 of Gillespie’s “Variations on a theme of Schubert calculus” 

We also recommend that students read the following papers, to gain exposure to the main topics of the summer school before the lectures start. Large portions of these papers will be mentioned during the lectures (without proof), so they are not strictly prerequisite material. 

Suggested Reading: 
(1) “How the Alternating Sign Matrix Conjecture was Solved,” by David Bressoud and James Propp
(2) Claudio Procesi, “Lie Groups”, p. 241-246
(3) Expository paper on the Grassmannian and its homogeneous coordinate ring by Drew A. Hudec

Recommended Preparatory Reading

Application Procedure

For eligibility and how to apply, see the Summer Graduate Schools homepage.