The African Diaspora Joint Mathematics Workshop (ADJOINT) is a two-week summer activity designed for researchers with a Ph.D. degree in the mathematical sciences who are interested in conducting research in a collegial environment.
The main objective of ADJOINT is to provide opportunities for in-person research collaboration to U.S. mathematicians, especially those from the African Diaspora, who will work in small groups with research leaders on various research projects.
Through this effort, MSRI aims to establish and promote research communities that will foster and strengthen research productivity and career development among its participants. The ADJOINT workshops are designed to catalyze research collaborations, provide support for conferences to increase the visibility of the researchers, and to develop a sense of community among the mathematicians who attend.
The end goal of this program is to enhance the mathematical sciences and its community by positively affecting the research and careers of African-American mathematicians and supporting their efforts to achieve full access and engagement in the broader research community.
The 2020 ADJOINT workshop took place June 15-26 virtually due to COVID-19.
About the Program
Each summer, three to five research leaders will each propose a research topic to be studied during a two-week workshop.
During the workshop, each participant will:
- conduct research at MSRI within a group of four to five mathematicians under the direction of one of the research leaders
- participate in professional enhancement activities provided by the onsite ADJOINT Director
- receive funding for two weeks of lodging, meals and incidentals, and one round-trip travel to Berkeley, CA
After the two-week workshop, each participant will:
- have the opportunity to further their research project with the team members including the research leader
- have access to funding to attend conference(s) or to meet with other team members to pursue the research project, or to present results
- become part of a network of research and career mentors
Eligibility
Applicants must be a U.S. citizen or permanent resident, possess a Ph.D. in the mathematical sciences, and be employed at a U.S. institution.
Selection Process
The guiding principle in selecting participants and establishing the groups is the creation of diverse teams whose members come from a variety of institutional types and career stages. The degree of potential positive impact on the careers of African-Americans in the mathematical sciences will be an important factor in the final decisions.
Summer 2020 Application Process and Deadline
ADJOINT 2020 took place virtually due to COVID-19. The research leaders and research topics can be found below.
Applications for ADJOINT 2020 were submitted via MathPrograms.
For reference, the 2020 application process required:
- a cover letter specifying which of the offered research projects they wish to be part of
- a CV
- a one-page personal statement that must address how the applicant’s participation will contribute to the goals of the program (e.g., why you are a good candidate for this workshop and what you hope to gain)
- a research statement, no longer than two pages, describing the the applicant's current research interests, and relevant past research activities, and how they relate to the project(s) of greatest interest to the applicant (e.g., what motivates your current interests and what is your relevant research background)
Due to funding restrictions, only U.S. citizens and permanent residents are eligible to apply. Applications which were submitted by February 7, 2020 received full consideration.
2020 Research Leaders and Topics
Tepper Gill (Howard University)
Analysis, PDEs, and Mathematical Physics
The center of mass for this research is a new class of separable Banach spaces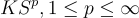 
, which contains each corresponding 
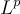space as a dense continuous embedding. (Click for full description)
Abba Gumel (Arizona State University)
Mathematics of the Transmission Dynamics and Control of the 2019 Novel Coronavirus
The world is currently facing a devastating pandemic of a novel Coronavirus (COVID-19), which started as an outbreak of pneumonia of unknown cause in Wuhan, China in December of 2019. As of April 26, 2020, COVID-19 (caused by the novel SARS-CoV-2 coronavirus) has spread to over 210 countries and territories, causing about three million infections and 207,000 deaths. In the absence of a safe and effective vaccine against COVID-19, and safe and approved antivirals, control and mitigation efforts are focused on the use of non-pharmaceutical interventions, such as social-distancing, quarantine, aggressive containment (i.e., rapid detection, isolation and contact-tracing of confirmed cases), use of face masks in public, etc. (Click for full description)
Ryan Hynd (University of Pennsylvania)
Hamilton-Jacobi equations in high dimensions
Hamilton-Jacobi equations (HJE) are partial differential equations which were first derived to study problems in classical mechanics. These equations have also played a central role in control and game theory. (Click for full description)
Bonita V. Saunders (National Institute of Standards and Technology)
Validated Numerical Computations of Mathematical Functions
During the late 1930s, 40s and 50s accurate tables of function values were calculated by human ‘computers’ to facilitate the evaluation of functions by interpolation. The advent of reliable computing machines, computer algebra systems, and computational packages diminished the need for such reference tables, but today’s researchers and software developers still need a way to confirm the accuracy of numerical codes that compute mathematical function values. (Click for full description)
Craig Sutton (Dartmouth College)
Explorations in Inverse Spectral Geometry
Inverse spectral geometry is the study of the relationship between the spectrum of a closed Riemannian manifold---i.e., the sequence of eigenvalue (counting multiplicities) of the associated Laplace-Beltrami operator---and its underlying geometry. (Click for full description)
ADJOINT Program Directors
- Dr. Edray Goins, Pomona College
- Dr. Caleb Ashley, University of Michigan
- Dr. Naiomi Cameron (Onsite Director), Spelman College
- Dr. Jacqueline Hughes-Oliver, North Carolina State University
- Dr. Anisah Nu’Man, Spelman College