Acknowledged as the premier center for collaborative mathematical research, MSRI organizes and hosts semester-length (or year-long) Programs that become the leading edge in that field of study. Mathematicians worldwide come to the Institute to engage in the research of classical fundamental mathematics, modern applied mathematics, statistics, computer science and other mathematical sciences.
MSRI invites the submission of proposals for full-year or half-year programs to be held at MSRI. Planning such programs is generally done about three years in advance. Except in extraordinary cases, a subject is the focus of a program not more than once in ten years.
Additional Resources
- Membership applications and deadlines
- Program-related workshops (conferences) held at MSRI
- Submitting a proposal for a future Program
The Complementary Program has a limited number of memberships that are open to mathematicians whose interests are not closely related to the core programs; special consideration is given to mathematicians who are partners of an invited member of a core program. Current Programs
Complementary Program 2025-26
Geometry and Dynamics for Discrete Subgroups of Higher Rank Lie Groups
Organizers: Martin Bridgeman (Boston College), LEAD Richard Canary (University of Michigan), Amir Mohammadi (University of California, Berkeley), LEAD Hee Oh (Yale University), Maria Beatrice Pozzetti (Università di Bologna), Jean-François Quint (CNRS - Université de Montpellier)
This research program will bring together two intellectual communities that have made significant advances in the study of discrete subgroups of higher rank semisimple Lie groups: the homogeneous dynamics community and the community studying geometric structures and Anosov groups.
Topological and Geometric Structures in Low Dimensions
Organizers: Ian Agol (University of California, Berkeley), Kenneth Bromberg (University of Utah), Sebastian Hensel (LMU München), Christopher Leininger (University of Illinois at Urbana-Champaign), Kathryn Mann (Cornell University), LEAD Yair Minsky (Yale University), Rachel Roberts (Washington University in St. Louis)
Low dimensional topology is a meeting place for many objects and ideas from diverse areas of mathematics, including foliation theory, geometry, and smooth and conformal dynamics. For instance, many foliations on 3-manifolds admit transverse flows, connecting (local) leafwise homeomorphisms to flow dynamics and the mapping class groups of the leaves. Leafwise conformal or hyperbolic structures can be approached through Teichmüller theory, and connect again to one-dimensional dynamics through "universal circles" organizing compactifications of all the leaves or of the flow space. Many of these ideas originate in work of Thurston but in recent years have diverged and are ripe for reconnection.
The program will bring together experts in all these fields together with younger researchers, who together can form new connections and open new areas for exploration.
Upcoming Programs
-
Representation Theory Under the Influence of Quantum Field Theory
Organizers: David Ben-Zvi (University of Texas, Austin), LEAD Tudor Dimofte (University of Edinburgh), Iva Halacheva (Northeastern University), LEAD Joel Kamnitzer (McGill University), Pavel Safronov (University of Edinburgh), Peng Shan (Tsinghua University) <p>Illustrated by Rok Gregoric</p>
<p>Illustrated by Rok Gregoric</p>The upcoming SLMath program is organized around key themes of “higher” quantization and mirror symmetry as they impact and elucidate a wide variety of questions in representation theory. The program will bring together experts and young researchers from algebra, geometry, physics and number theory to help develop and disseminate this unified vision of a rapidly evolving field, exploring the mathematical consequences of the examples, structures, and dualities discovered in physics.
Updated on Jul 16, 2025 09:07 AM PDT -
Motivic Homotopy Theory: Connections and Applications
Organizers: LEAD Aravind Asok (University of Southern California), Adrien Dubouloz (Universit'e de Poitiers), Elden Elmanto (University of Toronto, Scarborough), Dan Isaksen (Wayne State University), Paul Oestvær (Universita degli studi Milano), Anand Sawant (Tata Institute of Fundamental Research), Kirsten Wickelgren (Duke University), Maria Yakerson (Institut de Mathématiques de Jussieu)Tremendous progress has been made using motivic techniques in geometric questions for affine algebraic varieties, especially those involving algebraic vector bundles. Computations in classical algebraic topology have been improved by motivic techniques, e.g., related to the problem of computing homotopy groups of spheres. Moreover, the theory has identified new structures of interest in arithmetic situations. Transformative recent progress in motivic homotopy theory has only broadened the scope for potential applications of motivic techniques, as well as new avenues of interaction with other areas of mathematics. This program will build on previous successes, explaining the tools that have been developed and how to use them, analyzing questions of the sort described above and identifying new domains where motivic techniques will be successful.
Updated on Jul 16, 2025 09:24 AM PDT -
Complementary Program Fall 2026
The Complementary Program has a limited number of memberships that are open to mathematicians whose interests are not closely related to the core programs; special consideration is given to mathematicians who are partners of an invited member of a core program.
Updated on Jan 15, 2026 03:02 PM PST -
New Trends in Tropical Geometry
Organizers: Pierrick Bousseau (University of Georgia), Melody Chan (Brown University), Ilia Itenberg (Institut de Mathématiques de Jussieu - Paris Rive Gauche), Hannah Markwig (Eberhard-Karls-Universität Tübingen), LEAD Kris Shaw (University of Oslo) Tropical surfaces. Images courtesy of Lars Allermann.
Tropical surfaces. Images courtesy of Lars Allermann.Tropical geometry can be viewed as a degenerate version of algebraic geometry,where the role of algebraic varieties is played by certain polyhedral complexes. As the degeneration process, called tropicalization, preserves many fundamental properties, tropical geometry provides important bridges and an exchange of methods between algebraic geometry, symplectic geometry and convex geometry; these links have been extremely fruitful and gave rise to remarkable results during the last 20 years. The main focus of the program will be on the most significant recent developments in tropical geometry and its applications. The following topics are particularly influential in the area and will be central in the program:
- real aspects of tropical geometry;
- tropical mirror symmetry and non-Archimedean geometry;
- tropical phenomena in symplectic geometry;
- matroids, combinatorial and algebraic aspects;
- tropical moduli spaces;
- tropical geometry and A1-homotopy theory.
Updated on Jul 10, 2025 09:28 AM PDT -
Algebraic Combinatorics
Organizers: Sara Billey (University of Washington), LEAD Sylvie Corteel (Université de Paris VII (Denis Diderot); University of California, Berkeley), Philippe Di Francesco (University of Illinois at Urbana-Champaign), Cynthia Vinzant (University of Washington), Lauren Williams (Harvard University) Picture of an amplituhedron \mathcal{A}_{6,3,1}. (Figure 1 https://arxiv.org/pdf/1608.08288)
Picture of an amplituhedron \mathcal{A}_{6,3,1}. (Figure 1 https://arxiv.org/pdf/1608.08288)Algebraic combinatorics is an area of mathematics that employs methods in abstract algebra in combinatorial contexts, and that uses combinatorial methods to approach problems in algebra. Some important topics are symmetric functions, Young tableaux, matroids, Coxeter combinatorics. There are links to computer algebra (sage-combinat), number theory (L-functions), representation theory, and mathematical physics through Macdonald processes and integrability. The work on the totally positive Grassmannian also gave rise to beautiful results in mathematical physics: for example KP solitons and Scattering Amplitudes. Schubert calculus is an important part of algebraic combinatorics and is now at the frontier with k-Schur functions, which first came up in the theory of Macdonald polynomials.
Updated on Jul 10, 2025 09:39 AM PDT -
Inverse Problems and Applications
Organizers: Fioralba Cakoni (Rutgers University), Maarten de Hoop (Rice University), Anna Gilbert (Yale University), Katya Krupchyk (University of California, Irvine), Matti Lassas (University of Helsinki), LEAD Gunther Uhlmann (University of Washington)
Inverse problems (IP) arise in all fields of science and technology where a cause for an observed or desired effect is sought. In the last 50 years or so there has been substantial progress in the mathematical understanding of these problems but many questions remain open. The mathematics of these problems involves many areas in Mathematics including PDE, differential geometry, integral geometry, probability, statistics, complex analysis, numerical analysis, mathematical physics, data science, etc. Since the 2010 program at the then-Mathematical Sciences Research Institute (now Simons Laufer Mathematical Sciences Institute), there has been significant progress in inverse problems; many of the advances can be traced back to that program. However, there are still deep open questions remaining as well, some of which are discussed in this proposal. New research topics include the connection between IP and machine learning, IP for nonlinear equations, IP for nonlocal operators, and connections between statistics and IP.
Updated on Nov 06, 2025 12:15 PM PST -
Geometric Measure Theory
Organizers: Otis Chodosh (Stanford University), Camillo De Lellis (Institute for Advanced Study), LEAD Guido De Philippis (Hausdorff Research Institute for Mathematics, University of Bonn), Svitlana Mayboroda (University of Minnesota, Twin Cities), Robin Neumayer (Northwestern University), Luca Spolaor (University of California, San Diego), Zihui Zhao (Johns Hopkins University)
The field of Geoemtric Measure Theory (GMT)has become vast and many gaps between disparate areas have emerged. This thematic semester will bring together researchers from every corner of the field, to kick-start new interactions and discoveries. In light of the many exciting advancements and potential for future breakthroughs, this as a crucial moment to bring old and new members of the GMT community together. The program will encourage interactions between established experts, emerging researchers and students, allowing for the sharing of key idea that brought to the recent developments and helping to shape a research agenda for the future.
Updated on Jul 10, 2025 09:27 AM PDT -
Hodge Theory
Organizers: Ben Bakker (University of Illinois, Chicago), Robert Friedman (Columbia University), LEAD Radu Laza (State University of New York, Stony Brook), Colleen Robles (Duke University), Christian Schnell (State University of New York, Stony Brook), Junliang Shen (Yale University), Qizheng Yin (Fudan University) Stylized Hodge diamond
Stylized Hodge diamondHodge theory originated in the work of Hodge, Kodaira, and Weyl, who introduced analytic methods, particularly techniques from partial differential equations, to study the cohomology of compact Riemannian manifolds. Since then, Hodge theory has developed into a central and unifying framework in both complex and algebraic geometry. It plays a fundamental role in the study of algebraic cycles and moduli spaces, and it has deep connections with many other areas of mathematics, including model theory, symplectic geometry, singularity theory, D-modules and perverse sheaves, derived categories, representation theory, as well as arithmetic geometry and number theory. Over the past two decades, the field has witnessed remarkable progress, driven by the interaction of Hodge theory with tools and ideas from diverse areas.
Updated on Jan 20, 2026 11:37 AM PST -
Geometry and Combinatorics of Artin Groups and Arrangements
Organizers: Daniel Allcock (University of Texas, Austin), Christin Bibby (Louisiana State University), Ruth Charney (Brandeis University), Emanuele Delucchi (University of Applied Arts and Sciences of Southern Switzerland), Jon McCammond (University of California, Santa Barbara), LEAD Giovanni Paolini (Università di Bologna), Mario Salvetti (Università di Pisa)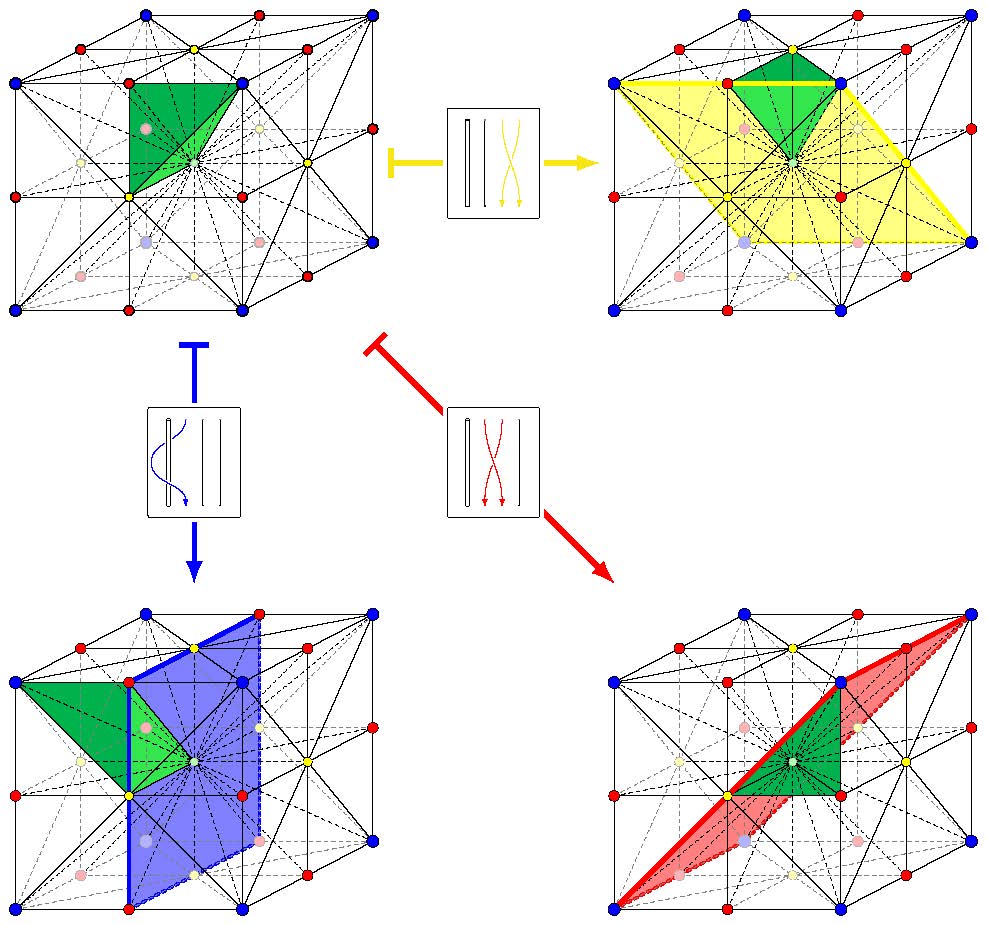 <p>Generators and their reflecting hyperplanes for the B3 Artin group</p>
<p>Generators and their reflecting hyperplanes for the B3 Artin group</p>Artin groups and arrangements are closely connected research areas at the crossroads of algebra, geometry and combinatorics. Recent progress on classical problems and the development of new techniques has led to intense activity both internally and in connection with adjacent research areas. Our program will build upon recent breakthroughs, address foundational questions and foster exchange between experts. We aim at strengthening the emerging connections with other research areas and encouraging junior researchers to engage with this broader landscape.
Updated on Jan 20, 2026 11:28 AM PST
Past Programs
-
Program Recent Trends in Stochastic Partial Differential Equations
Organizers: Sandra Cerrai (University of Maryland), Yu Gu (University of Maryland), Massimiliano Gubinelli (University of Oxford), Davar Khoshnevisan (University of Utah), Andrea Nahmod (University of Massachusetts, Amherst), Hao Shen (University of Wisconsin-Madison), LEAD Lorenzo Zambotti (Sorbonne Université)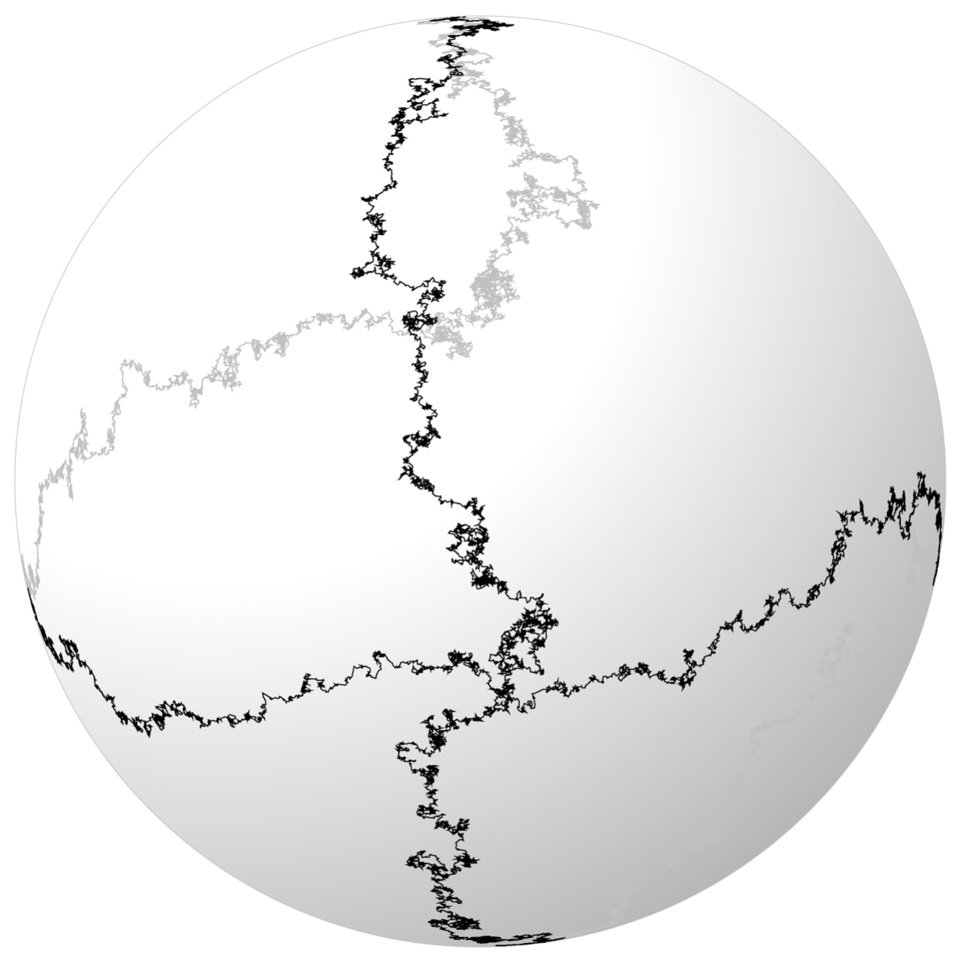 Solution to the geometric stochastic heat equation on the sphere at a fixed time
Solution to the geometric stochastic heat equation on the sphere at a fixed timeThe topic Singular Stochastic Partial Differential Equations (singular SPDE) has rapidly grown to be an active research area at the interface of Stochastic Analysis and PDEs on one hand, and Mathematical Physics on the other hand. During this decade we have witnessed a series of tremendous breakthroughs in the solution theories of SPDEs, universality problems, large-scale asymptotic behaviors of solutions, and foundational relations with quantum field theories and geometry. Many long-standing problems have been resolved via newly developed methods – notably the theories of regularity structures and paracontrolled distributions – and deep connections with other fields are quickly emerging.
It is a natural time to convene a large-scale semester program.
Updated on Jul 09, 2024 04:18 PM PDT -
Program Kinetic Theory: Novel Statistical, Stochastic and Analytical Methods
Organizers: Laurent Desvillettes (Université Paris Cité), Irene M. Gamba (University of Texas, Austin), François Golse (Centre de Mathématiques Laurent Schwartz, École Polytechnique), Cyril Imbert (Centre National de la Recherche Scientifique (CNRS); Université Paris Cité), LEAD Pierre-Emmanuel Jabin (Pennsylvania State University), Qin Li (University of Wisconsin-Madison), Chiara Saffirio (Universität Basel), Weiran Sun (Simon Fraser University), Lexing Ying (Stanford University) Top: Neutrino interactions and neutrino-atom interactions. Bottom: Collision of two "waves"
Top: Neutrino interactions and neutrino-atom interactions. Bottom: Collision of two "waves"The focus of the proposed program is on so-called kinetic equations, describing the evolution of the of many-particle interacting systems. These models have the form of statistical flows, with their solutions being either a single or multiple point probability density functions or measures, supported in a space of attributes. The attributes are problem-dependent and can be molecular velocity, energy, opinion, wealth, and many others. The flow then predicts the evolution of the probability measure in time, position in space, and the interchanging of the particles' states by the transition probability.
The program will strive to give an overview of the novel mathematical tools used in kinetic theory through a broad range of classical and more recent applications.
Updated on Jul 23, 2025 01:24 PM PDT -
Program Complementary Program 2024-25
The Complementary Program has a limited number of memberships that are open to mathematicians whose interests are not closely related to the core programs; special consideration is given to mathematicians who are partners of an invited member of a core program.
Updated on Nov 03, 2023 03:25 PM PDT -
Program Extremal Combinatorics
Organizers: LEAD David Conlon (California Institute of Technology), LEAD Jacob Fox (Stanford University), Penny Haxell (University of Waterloo), János Pach (Alfréd Rényi Institute of Mathematics), Maya Stein (Universidad de Chile), Andrew Suk (University of California, San Diego)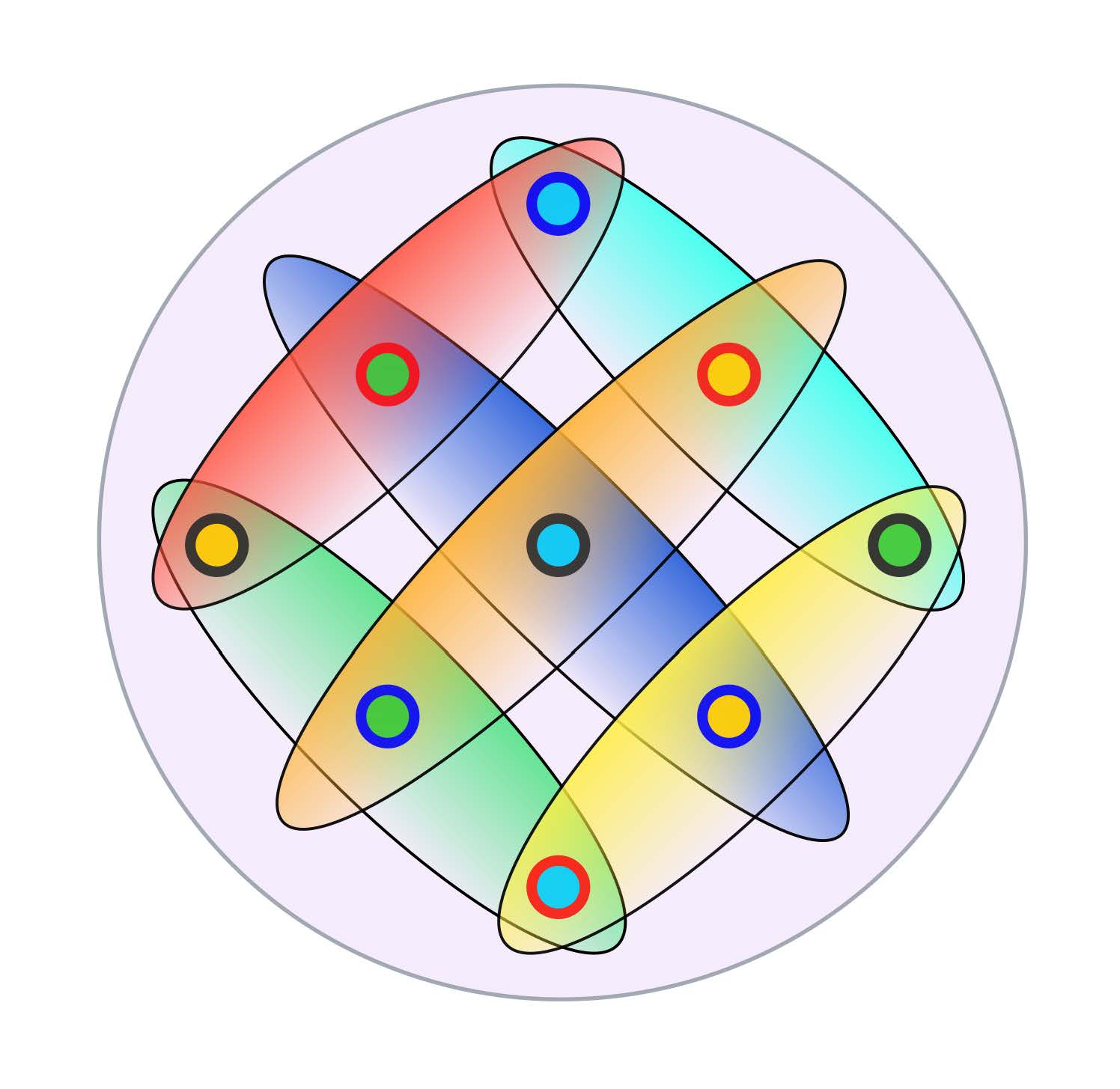
Extremal combinatorics concerns itself with problems about how large or small a finite collection of objects can be while satisfying certain conditions. Questions of this type arise naturally across mathematics, so this area has close connections and interactions with a broad array of other fields, including number theory, group theory, model theory, probability, statistical physics, optimization, and theoretical computer science.
Updated on Dec 16, 2024 03:09 PM PST -
Program Probability and Statistics of Discrete Structures
Organizers: Louigi Addario-Berry (McGill University), Christina Goldschmidt (University of Oxford), Po-Ling Loh (University of Cambridge), Gábor Lugosi (Pompeu Fabra University), Dana Randall (Georgia Institute of Technology), LEAD Remco van der Hofstad (Technische Universiteit Eindhoven) The minimum spanning tree of 100,000 uniformly random points. Colors encode graph distance from the root, which is red. Black points are those whose removal would disconnect at least 5% of the points from the rest.
The minimum spanning tree of 100,000 uniformly random points. Colors encode graph distance from the root, which is red. Black points are those whose removal would disconnect at least 5% of the points from the rest.This program is devoted to the study of the probabilistic and statistical properties of such networks. Central tools include graphon theory for dense graphs, local weak convergence for sparse graphs, and scaling limits for the critical behavior of graphs or stochastic processes on them. The program is aimed at pure and applied mathematicians interested in network problems.
Updated on Dec 19, 2024 09:02 AM PST -
Program Special Geometric Structures and Analysis
Organizers: Eleonora Di Nezza (Institut de Mathématiques de Jussieu; École Normale Supérieure), LEAD Mark Haskins (Duke University), Tristan Riviere (ETH Zurich), Song Sun (Zhejiang University; University of California, Berkeley), Xuwen Zhu (Northeastern University) “Plateau’s Memory ” (by A. van der Net): A soap film with singularities
“Plateau’s Memory ” (by A. van der Net): A soap film with singularitiesThis program sits at the intersection between differential geometry and analysis but also connects to several other adjacent mathematical fields and to theoretical physics. Differential geometry aims to answer questions about very regular geometric objects (smooth Riemannian manifolds) using the tools of differential calculus. A fundamental object is the curvature tensor of a Riemannian metric: an algebraically complicated object that involves 2nd partial derivatives of the metric. Many questions in differential geometry can therefore be translated into questions about the existence or properties of the solutions of systems of (often) nonlinear partial differential equations (PDEs). The PDE systems that arise in geometry have historically stimulated the development of powerful new analytic methods. In most cases the nonlinearity of these systems makes ‘closed form’ expressions for a solution impossible: instead more abstract methods must be employed.
Updated on Apr 10, 2025 01:21 PM PDT -
Program New Frontiers in Curvature: Flows, General Relativity, Minimal Submanifolds, and Symmetry
Organizers: LEAD Ailana Fraser (University of British Columbia), Lan-Hsuan Huang (University of Connecticut), Richard Schoen (University of California, Irvine), LEAD Catherine Searle (Wichita State University), Lu Wang (Yale University), Guofang Wei (University of California, Santa Barbara) Soap bubble: equilibrium solution of the mean curvature flow and constant curvature surface.
Soap bubble: equilibrium solution of the mean curvature flow and constant curvature surface.Geometry, PDE, and Relativity are subjects that have shown intriguing interactions in the past several decades, while simultaneously diverging, each with an ever growing number of branches. Recently, several major breakthroughs have been made in each of these fields using techniques and ideas from the others.
This program is aimed at connecting various branches of Geometry, PDE, and Relativity and at enhancing collaborations across these disciplines and will include four main topics: Geometric Flows, Geometric problems in Mathematical Relativity, Global Riemannian Geometry, and Minimal Submanifolds. Specifically the program focuses on a central goal, which is to advance our knowledge toward Riemannian (sub)manifolds under geometric conditions, such as curvature lower bounds, by developing techniques in, for example, geometric flows and minimal submanifolds and further fostering new connections.
Updated on Sep 19, 2024 09:19 AM PDT -
Program Quantum Symmetries Reunion
 The study of tensor categories involves the interplay of representation theory, combinatorics, number theory, and low dimensional topology (from a string diagram calculation, describing the 3-dimensional bordism 2-category [arXiv:1411.0945]).
The study of tensor categories involves the interplay of representation theory, combinatorics, number theory, and low dimensional topology (from a string diagram calculation, describing the 3-dimensional bordism 2-category [arXiv:1411.0945]).Symmetry, as formalized by group theory, is ubiquitous across mathematics and science. Classical examples include point groups in crystallography, Noether's theorem relating differentiable symmetries and conserved quantities, and the classification of fundamental particles according to irreducible representations of the Poincaré group and the internal symmetry groups of the standard model. However, in some quantum settings, the notion of a group is no longer enough to capture all symmetries. Important motivating examples include Galois-like symmetries of von Neumann algebras, anyonic particles in condensed matter physics, and deformations of universal enveloping algebras. The language of tensor categories provides a unified framework to discuss these notions of quantum symmetry.
Updated on Jun 27, 2024 12:12 PM PDT -
Program Complementary Program 2023-24
The Complementary Program has a limited number of memberships that are open to mathematicians whose interests are not closely related to the core programs; special consideration is given to mathematicians who are partners of an invited member of a core program.
Updated on Sep 26, 2023 11:36 AM PDT -
Program Noncommutative Algebraic Geometry
Organizers: Wendy Lowen (Universiteit Antwerpen), Alex Perry (University of Michigan), LEAD Alexander Polishchuk (University of Oregon), Susan Sierra (University of Edinburgh), Michel VAN DEN BERGH (Hasselt University), Špela Špenko (Université Libre de Bruxelles) Optical illusion staircase
Optical illusion staircaseDerived categories of coherent sheaves on algebraic varieties were originally conceived as technical tools for studying cohomology, but have since become central objects in fields ranging from algebraic geometry to mathematical physics, symplectic geometry, and representation theory. Noncommutative algebraic geometry is based on the idea that any category sufficiently similar to the derived category of a variety should be regarded as (the derived category of) a “noncommutative algebraic variety”; examples include semiorthogonal components of derived categories, categories of matrix factorizations, and derived categories of noncommutative dg-algebras. This perspective has led to progress on old problems, as well as surprising connections between seemingly unrelated areas. In recent years there have been great advances in this domain, including new tools for constructing semiorthogonal decompositions and derived equivalences, progress on conjectures relating birational geometry and singularities to derived categories, constructions of moduli spaces from noncommutative varieties, and instances of homological mirror symmetry for noncommutative varieties. The goal of this program is to explore and expand upon these developments.
Updated on Jan 22, 2024 12:22 PM PST -
Program Commutative Algebra
Organizers: Aldo Conca (Università di Genova), Steven Cutkosky (University of Missouri), LEAD Claudia Polini (University of Notre Dame), Claudiu Raicu (University of Notre Dame), Steven Sam (University of California, San Diego), Kevin Tucker (University of Illinois at Chicago), Claire Voisin (Collège de France; Institut de Mathématiques de Jussieu)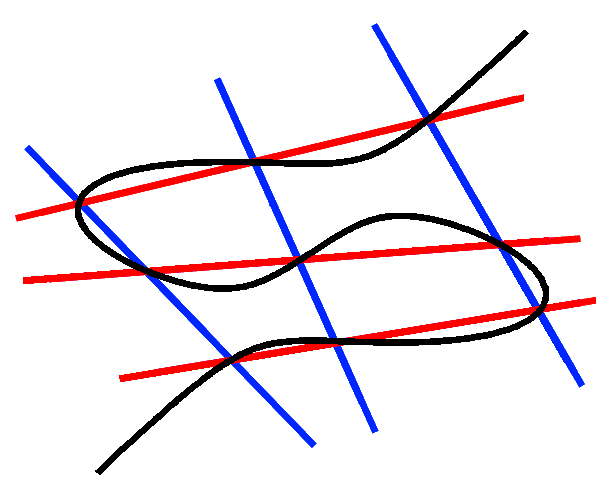 Image for theorem about 9 point on cubic curve, the special case of Cayley–Bacharach theorem.
Image for theorem about 9 point on cubic curve, the special case of Cayley–Bacharach theorem.Commutative algebra is, in its essence, the study of algebraic objects, such as rings and modules over them, arising from polynomials and integral numbers. It has numerous connections to other fields of mathematics including algebraic geometry, algebraic number theory, algebraic topology and algebraic combinatorics. Commutative Algebra has witnessed a number of spectacular developments in recent years, including the resolution of long-standing problems, with new techniques and perspectives leading to an extraordinary transformation in the field. The main focus of the program will be on these developments. These include the recent solution of Hochster's direct summand conjecture in mixed characteristic that employs the theory of perfectoid spaces, a new approach to the Buchsbaum--Eisenbud--Horrocks conjecture on the Betti numbers of modules of finite length, recent progress on the study of Castelnuovo--Mumford regularity, the proof of Stillman's conjecture and ongoing work on its effectiveness, a novel strategy to Green's conjecture on the syzygies of canonical curves based on the study of Koszul modules and their generalizations, new developments in the study of various types of multiplicities, theoretical and computational aspects of Gröbner bases, and the implicitization problem for Rees algebras and its applications.
Updated on Jan 02, 2024 10:36 AM PST -
Program Algorithms, Fairness, and Equity
Organizers: Vincent Conitzer (Carnegie Mellon University), Moon Duchin (Tufts University), Bettina Klaus (University of Lausanne), Jonathan Mattingly (Duke University), LEAD Wesley Pegden (Carnegie Mellon University)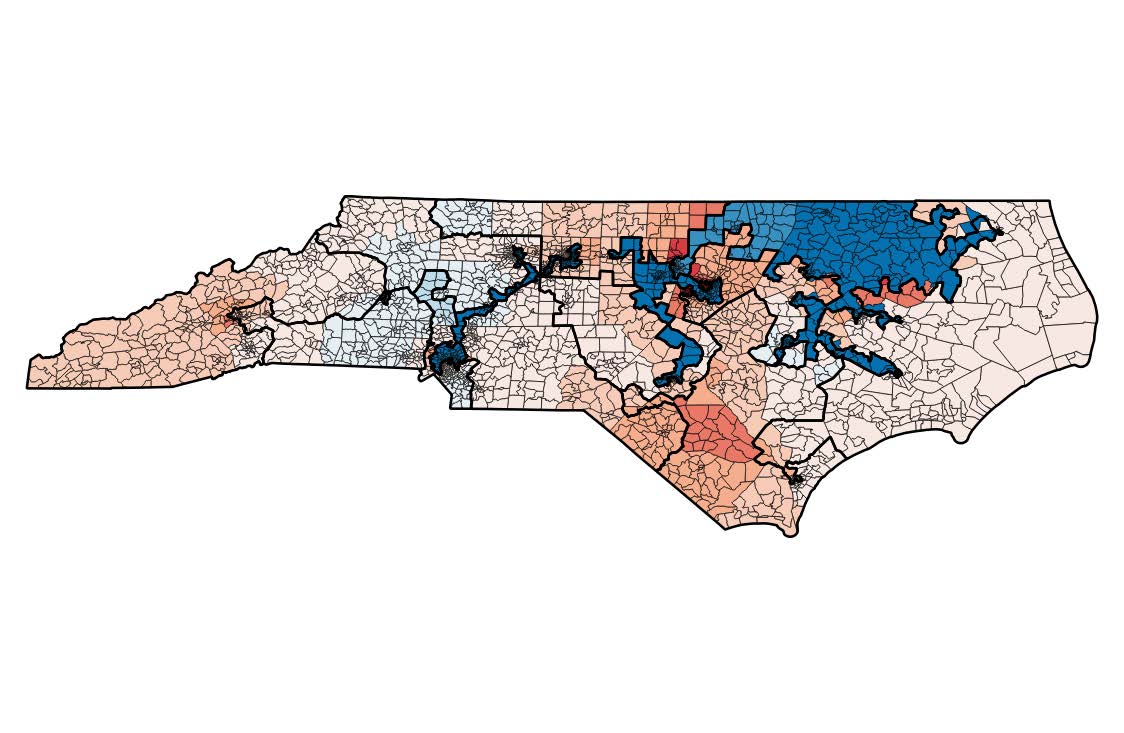 <p>A graphical representation of a Markov Chain fairness analysis of a political districting in North Carolina from Chin, Herschlag, Mattingly</p>
<p>A graphical representation of a Markov Chain fairness analysis of a political districting in North Carolina from Chin, Herschlag, Mattingly</p>This program aims to bring together researchers working at the interface of fairness and computation. This interface has been the site of intensive research effort in mechanism design, in research on partitioning problems related to political districting problems, and in research on ways to address issues of fairness and equity in the context of machine learning algorithms.
These areas each approach the relationship between mathematics and fairness from a distinct perspective. In mechanism design, algorithms are a tool to achieve outcomes with mathematical guarantees of various notions of fairness. In machine learning, we perceive failures of fairness as an undesirable side effect of learning approaches, and seek mathematical approaches to understand and mitigate these failures. And in partitioning problems like political districting, we often seek mathematical tools to evaluate the fairness of human decisions.
This program will explore progress in these areas while also providing a venue for overlapping perspectives. The topics workshop “Randomization, neutrality, and fairness” will explore the common role randomness and probability has played in these lines of work.
Updated on Aug 24, 2023 07:26 AM PDT -
Program Mathematics and Computer Science of Market and Mechanism Design
Organizers: Martin Bichler (TU München), Péter Biró (KRTK – Institute of Economics), Michal Feldman (Tel-Aviv University), Nicole Immorlica (Microsoft Research), LEAD Scott Kominers (Harvard Business School), Shengwu Li (Harvard University), Paul Milgrom (Stanford University), Alvin Roth (Stanford University), Eva Tardos (Cornell University)
In recent years, economists and computer scientists have collaborated with mathematicians, operations research experts, and practitioners to improve the design and operations of real-world marketplaces. Such work relies on robust feedback between theory and practice, inspiring new mathematics closely linked – and directly applicable – to market and mechanism design questions. This cross-disciplinary program seeks to expand the domains in which existing market design solutions can be applied; address foundational questions regarding our ways of developing and evaluating mechanisms; and build useful analytic frameworks for applying theory to practical marketplace design.
Updated on Oct 18, 2023 09:04 AM PDT -
Program Complementary Program 2022-23
Updated on Aug 07, 2023 05:47 PM PDT -
Program Mathematical Problems in Fluid Dynamics, part 2
Organizers: Thomas Alazard (Ecole Normale Supérieure Paris-Saclay; Centre National de la Recherche Scientifique (CNRS)), Hajer Bahouri (Laboratoire Jacques-Louis Lions; Centre National de la Recherche Scientifique (CNRS)), Mihaela Ifrim (University of Wisconsin-Madison), Igor Kukavica (University of Southern California), David Lannes (Institut de Mathématiques de Bordeaux; Centre National de la Recherche Scientifique (CNRS)), Daniel Tataru (University of California, Berkeley)PROGRAM DESCRIPTION
Fluid dynamics is one of the classical areas of partial differential equations, and has been the subject of extensive research over hundreds of years. It is perhaps one of the most challenging and exciting fields of scientific pursuit simply because of the complexity of the subject and the endless breadth of applications.
The focus of the program is on incompressible fluids, where water is a primary example. The fundamental equations in this area are the well-known Euler equations for inviscid fluids, and the Navier-Stokes equations for the viscous fluids. Relating the two is the problem of the zero viscosity limit, and its connection to the phenomena of turbulence. Water waves, or more generally interface problems in fluids, represent another target area for the program. Both theoretical and numerical aspects will be considered.
Updated on Oct 20, 2023 09:39 AM PDT -
Program Simons Bridge Postdoctoral Fellowship 2022/23
Updated on Feb 10, 2022 10:34 AM PST -
Program Diophantine Geometry
Organizers: Jennifer Balakrishnan (Boston University), Mirela Ciperiani (University of Texas, Austin), Philipp Habegger (University of Basel), Wei Ho (Institute for Advanced Study), LEAD Hector Pasten (Pontificia Universidad Católica de Chile), Yunqing Tang (University of California, Berkeley), Shou-Wu Zhang (Princeton University)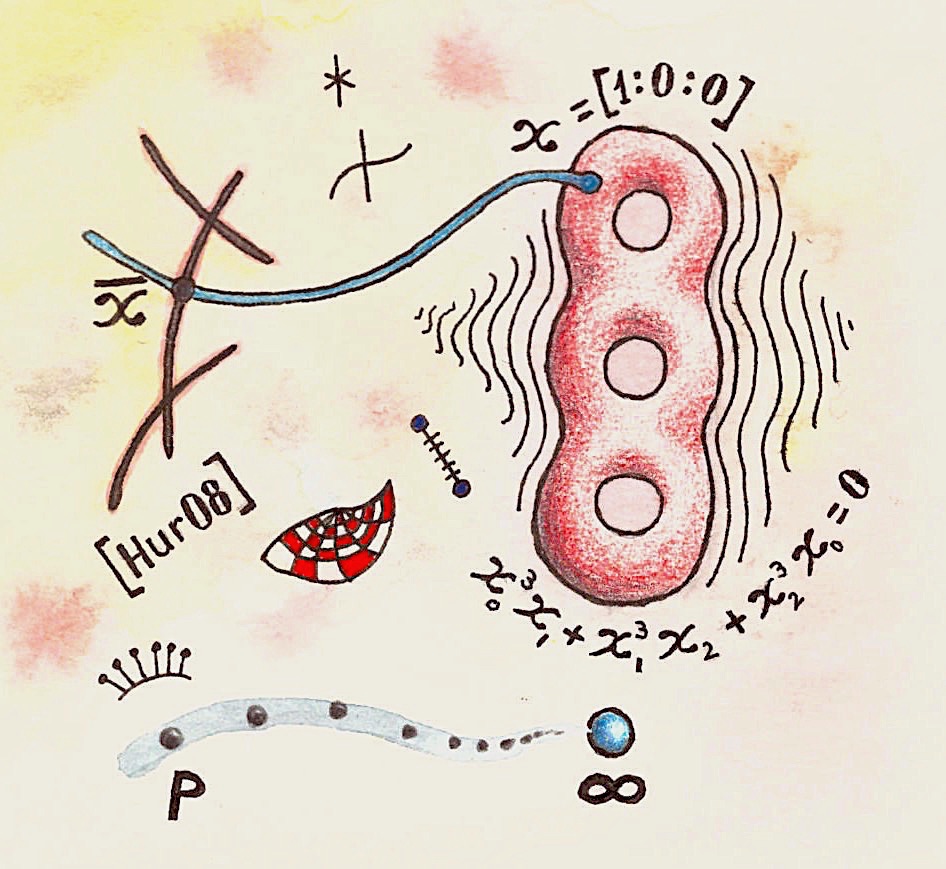 A rational point on a curve of genus 3
A rational point on a curve of genus 3While the study of rational solutions of diophantine equations initiated thousands of years ago, our knowledge on this subject has dramatically improved in recent years. Especially, we have witnessed spectacular progress in aspects such as height formulas and height bounds for algebraic points, automorphic methods, unlikely intersection problems, and non-abelian and p-adic approaches to algebraic degeneracy of rational points. All these groundbreaking advances in the study of rational and algebraic points in varieties will be the central theme of the semester program “Diophantine Geometry” at MSRI. The main purpose of this program is to bring together experts as well as enthusiastic young researchers to learn from each other, to initiate and continue collaborations, to update on recent breakthroughs, and to further advance the field by making progress on fundamental open problems and by developing further connections with other branches of mathematics. We trust that younger mathematicians will greatly contribute to the success of the program with their new ideas. It is our hope that this program will provide a unique opportunity for women and underrepresented groups to make outstanding contributions to the field, and we strongly encourage their participation.
Updated on Oct 20, 2023 10:29 AM PDT -
Program Algebraic Cycles, L-Values, and Euler Systems
Organizers: Henri Darmon (McGill University), Ellen Eischen (University of Oregon), LEAD Benjamin Howard (Boston College), David Loeffler (UniDistance Suisse), Christopher Skinner (Princeton University), Sarah Zerbes (ETH Zürich), Wei Zhang (Massachusetts Institute of Technology)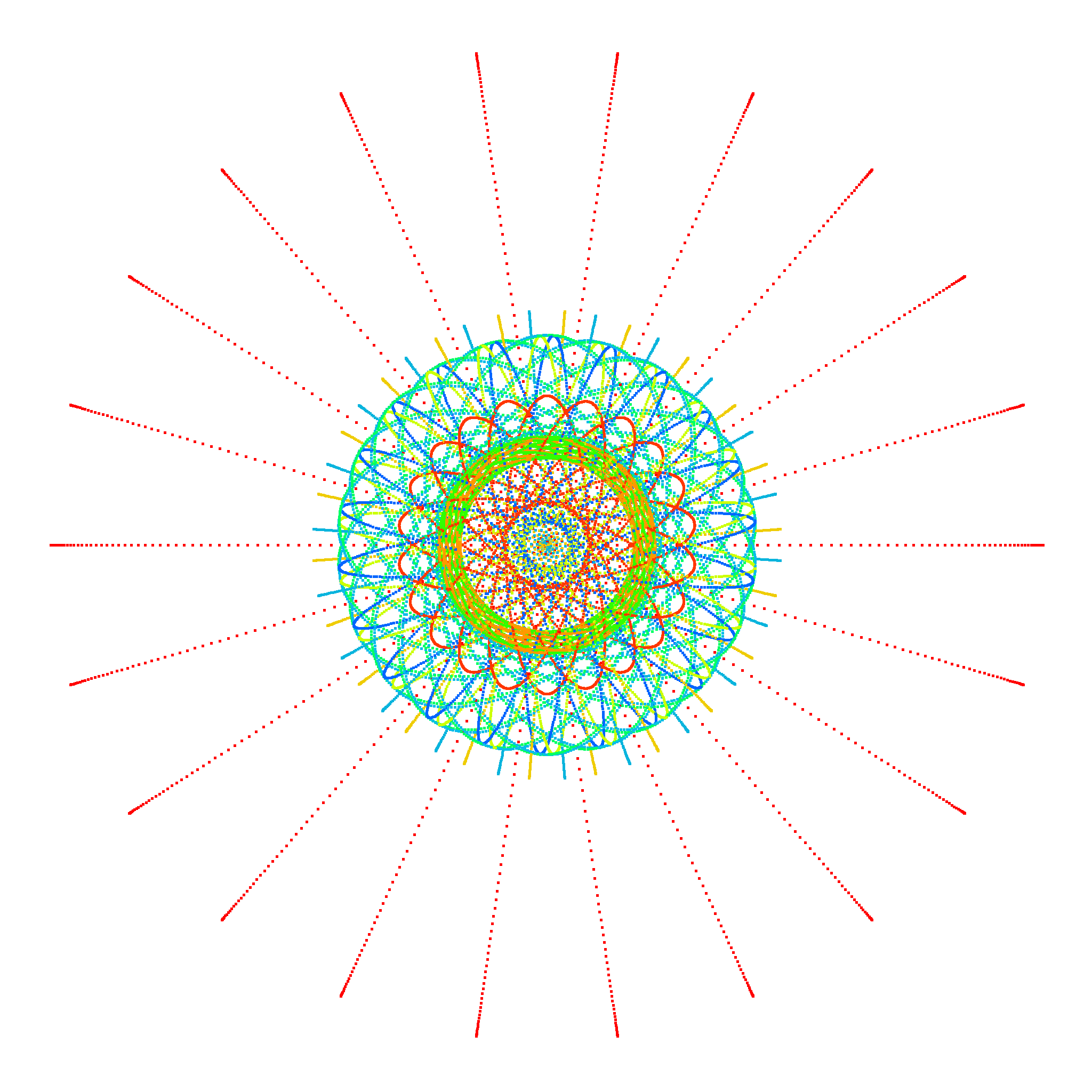 Some Gaussian periods for the 255,255-th cyclotomic extension. Image credit: E. Eischen, based on earlier work by W. Duke, S. R. Garcia, T. Hyde, and R. Lutz
Some Gaussian periods for the 255,255-th cyclotomic extension. Image credit: E. Eischen, based on earlier work by W. Duke, S. R. Garcia, T. Hyde, and R. LutzThe fundamental conjecture of Birch and Swinnerton-Dyer relating the Mordell–Weil ranks of elliptic curves to their L-functions is one of the most important and motivating problems in number theory. It resides at the heart of a collection of important conjectures (due especially to Deligne, Beilinson, Bloch and Kato) that connect values of L-functions and their leading terms to cycles and Galois cohomology groups.
The study of special algebraic cycles on Shimura varieties has led to progress in our understanding of these conjectures. The arithmetic intersection numbers and the p-adic regulators of special cycles are directly related to the values and derivatives of L-functions, as shown in the pioneering theorem of Gross-Zagier and its p-adic avatars for Heegner points on modular curves. The cohomology classes of special cycles (and related constructions such as Eisenstein classes) form the foundation of the theory of Euler systems, providing one of the most powerful methods known to prove vanishing or finiteness results for Selmer groups of Galois representations.
The goal of this semester is to bring together researchers working on different aspects of this young but fast-developing subject, and to make progress on understanding the mysterious relations between L-functions, Euler systems, and algebraic cycles.
Updated on Oct 20, 2023 10:26 AM PDT -
Program Analytic and Geometric Aspects of Gauge Theory
Organizers: Laura Fredrickson (University of Texas, Austin), Rafe Mazzeo (Stanford University), Tomasz Mrowka (Massachusetts Institute of Technology), Laura Schaposnik (University of Illinois at Urbana-Champaign), LEAD Thomas Walpuski (Humboldt-Universität)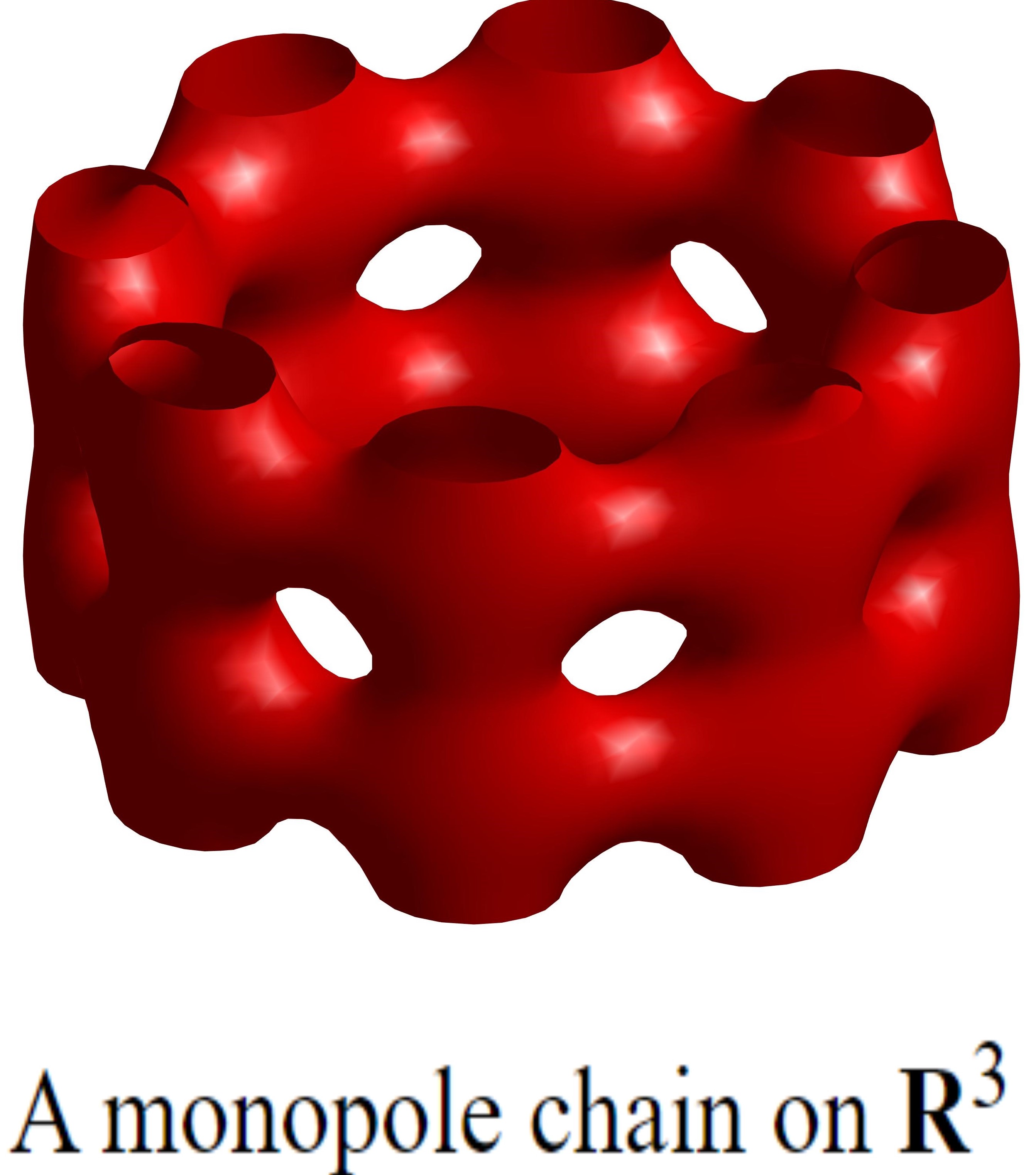
The mathematics and physics around gauge theory have, since their first interaction in the mid 1970’s, prompted tremendous developments in both mathematics and physics. Deep and fundamental tools in partial differential equations have been developed to provide rigorous foundations for the mathematical study of gauge theories. This led to ongoing revolutions in the understanding of manifolds of dimensions 3 and 4 and presaged the development of symplectic topology. Ideas from quantum field theory have provided deep insights into new directions and conjectures on the structure of gauge theories and suggested many potential applications. The focus of this program will be those parts of gauge theory which hold promise for new applications to geometry and topology and require development of new analytic tools for their study.
Updated on Oct 20, 2023 10:50 AM PDT -
Program Floer Homotopy Theory
Organizers: Mohammed Abouzaid (Stanford University), Andrew Blumberg (Columbia University), Kristen Hendricks (Rutgers University), Robert Lipshitz (University of Oregon), LEAD Ciprian Manolescu (Stanford University), Nathalie Wahl (University of Copenhagen)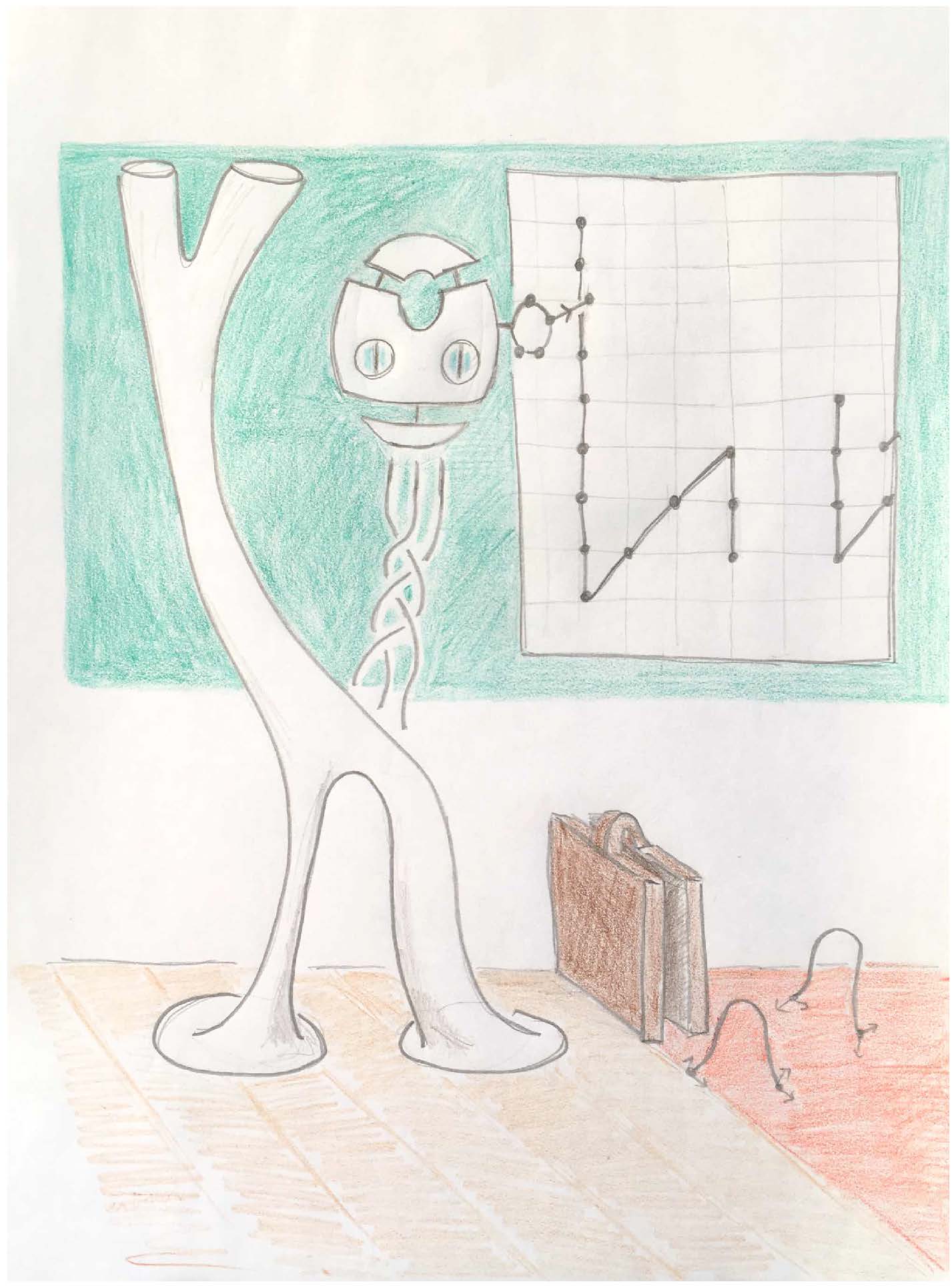 Illustrated by Nathalie Wahl
Illustrated by Nathalie WahlThe development of Floer theory in its early years can be seen as a parallel to the emergence of algebraic topology in the first half of the 20th century, going from counting invariants to homology groups, and beyond that to the construction of algebraic structures on these homology groups and their underlying chain complexes. In continuing work that started in the latter part of the 20th century, algebraic topologists and homotopy theorists have developed deep methods for refining these constructions, motivated in large part by the application of understanding the classification of manifolds. The goal of this program is to relate these developments to Floer theory with the dual aims of (i) making progress in understanding symplectic and low-dimensional topology, and (ii) providing a new set of geometrically motivated questions in homotopy theory.
Updated on Oct 20, 2023 10:47 AM PDT -
Program Definability, Decidability, and Computability in Number Theory, part 2
Organizers: Valentina Harizanov (George Washington University), Barry Mazur (Harvard University), Russell Miller (Queens College, CUNY; CUNY, Graduate Center), Jonathan Pila (University of Oxford), Thomas Scanlon (University of California, Berkeley), Alexandra Shlapentokh (East Carolina University) Title page of Diophantus' Arithmetica - ETH Zurich
Title page of Diophantus' Arithmetica - ETH ZurichThis program is focused on the two-way interaction of logical ideas and techniques, such as definability from model theory and decidability from computability theory, with fundamental problems in number theory. These include analogues of Hilbert's tenth problem, isolating properties of fields of algebraic numbers which relate to undecidability, decision problems around linear recurrence and algebraic differential equations, the relation of transcendence results and conjectures to decidability and decision problems, and some problems in anabelian geometry and field arithmetic. We are interested in this specific interface across a range of problems and so intend to build a semester which is both more topically focused and more mathematically broad than a typical MSRI program.
Updated on Dec 21, 2021 09:51 AM PST -
Program Complementary Program 2021-22
The Complementary Program has a limited number of memberships that are open to mathematicians whose interests are not closely related to the core programs; special consideration is given to mathematicians who are partners of an invited member of a core program.
Updated on May 03, 2022 02:54 PM PDT -
Program Simons Bridge Postdoctoral Fellowship 2021/22
Updated on Feb 10, 2022 10:34 AM PST -
Program Higher Categories and Categorification, Part Two
Organizers: David Ayala (Montana State University), Clark Barwick (University of Edinburgh), David Nadler (Northwestern University), LEAD Emily Riehl (Johns Hopkins University), Marcy Robertson (University of Melbourne), Peter Teichner (Max-Planck-Institut für Mathematik), Dominic Verity (Macquarie University)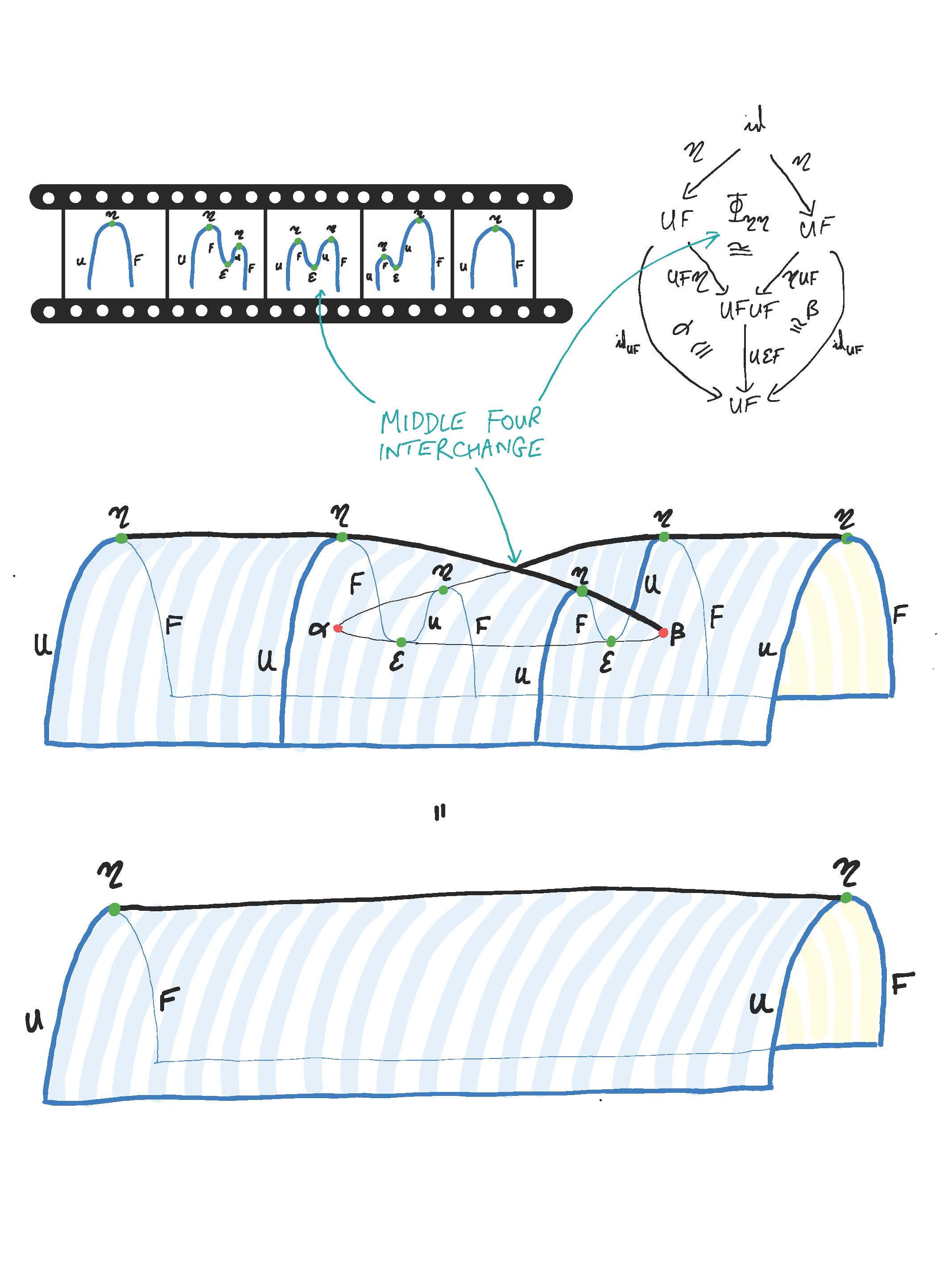 swallowtail identity
swallowtail identityThough many of the ideas in higher category theory find their origins in homotopy theory — for instance as expressed by Grothendieck’s “homotopy hypothesis” — the subject today interacts with a broad spectrum of areas of mathematical research. Unforeseen descent, or local-to-global formulas, for familiar objects can be articulated in terms of higher invertible morphisms. Compatible associative deformations of a sequence of maps of spaces, or derived schemes, can putatively be represented by higher categories, as Koszul duality for E_n-algebras suggests. Higher categories offer unforeseen characterizing universal properties for familiar constructions such as K-theory. Manifold theory is natively connected to higher category theory and adjunction data, a connection that is most famously articulated by the recently proven Cobordism Hypothesis.
In parallel, the idea of "categorification'' is playing an increasing role in algebraic geometry, representation theory, mathematical physics, and manifold theory, and higher categorical structures also appear in the very foundations of mathematics in the form of univalent foundations and homotopy type theory. A central mission of this semester will be to mitigate the exorbitantly high "cost of admission'' for mathematicians in other areas of research who aim to apply higher categorical technology and to create opportunities for potent collaborations between mathematicians from these different fields and experts from within higher category theory.Updated on Jun 06, 2022 12:39 PM PDT -
Program The Analysis and Geometry of Random Spaces
Organizers: LEAD Mario Bonk (University of California, Los Angeles), Joan Lind (University of Tennessee), Steffen Rohde (University of Washington), Eero Saksman (University of Helsinki), Fredrik Viklund (Royal Institute of Technology), Jang-Mei Wu (University of Illinois at Urbana-Champaign)
This program is devoted to the investigation of universal analytic and geometric objects that arise from natural probabilistic constructions, often motivated by models in mathematical physics. Prominent examples for recent developments are the Schramm-Loewner evolution, the continuum random tree, Bernoulli percolation on the integers, random surfaces produced by Liouville Quantum Gravity, and Jordan curves and dendrites obtained from random conformal weldings and laminations. The lack of regularity of these random structures often results in a failure of classical methods of analysis. One goal of this program is to enrich the analytic toolbox to better handle these rough structures.
Updated on Dec 21, 2021 12:37 PM PST -
Program Complex Dynamics: from special families to natural generalizations in one and several variables
Organizers: LEAD Sarah Koch (University of Michigan), Jasmin Raissy (Institut de Mathématiques de Bordeaux), Dierk Schleicher (Université d'Aix-Marseille (AMU)), Mitsuhiro Shishikura (Kyoto University), Dylan Thurston (Boston College) The mating of these two dendritic Julia sets is equal to the Julia set of a rational map of degree 2; that Julia set is equal to the entire Riemann sphere. Picture by Arnaud Chéritat
The mating of these two dendritic Julia sets is equal to the Julia set of a rational map of degree 2; that Julia set is equal to the entire Riemann sphere. Picture by Arnaud ChéritatHolomorphic dynamics is a vibrant field of mathematics that has seen profound progress over the past 40 years. It has numerous interconnections to other fields of mathematics and beyond.
Our semester will focus on three selected classes of dynamical systems: rational maps (postcritically finite and beyond); transcendental maps; and maps in several complex variables. We will put particular emphasis on the interactions between each these, and on connections with adjacent areas of mathematics.
Updated on Oct 20, 2023 01:06 PM PDT -
Program Universality and Integrability in Random Matrix Theory and Interacting Particle Systems
Organizers: LEAD Ivan Corwin (Columbia University), Percy Deift (New York University, Courant Institute), Ioana Dumitriu (University of California, San Diego), Alice Guionnet (École Normale Supérieure de Lyon), Alexander Its (Indiana University--Purdue University), Herbert Spohn (Technische Universität München), Horng-Tzer Yau (Harvard University)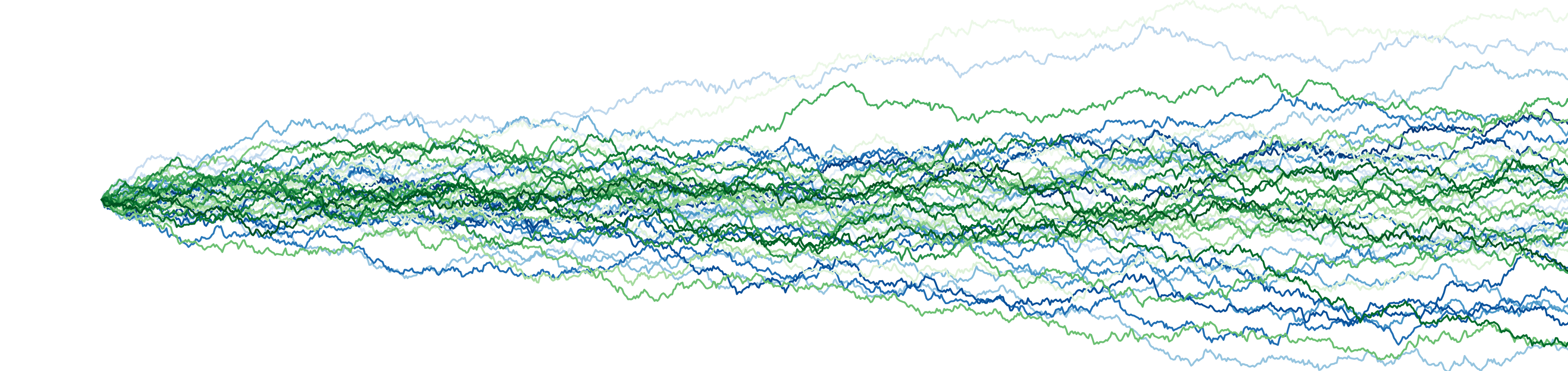
The past decade has seen tremendous progress in understanding the behavior of large random matrices and interacting particle systems. Complementary methods have emerged to prove universality of these behaviors, as well as to probe their precise nature using integrable, or exactly solvable models. This program seeks to reinforce and expand the fruitful interaction at the interface of these areas, as well as to showcase some of the important developments and applications of the past decade.
Updated on Oct 20, 2023 01:11 PM PDT -
Program Complementary Program 2020-21
The Complementary Program has a limited number of memberships that are open to mathematicians whose interests are not closely related to the core programs; special consideration is given to mathematicians who are partners of an invited member of a core program.
Updated on Jul 14, 2021 09:02 AM PDT -
Program Mathematical problems in fluid dynamics
Organizers: Thomas Alazard (Ecole Normale Supérieure Paris-Saclay; Centre National de la Recherche Scientifique (CNRS)), Hajer Bahouri (Laboratoire Jacques-Louis Lions; Centre National de la Recherche Scientifique (CNRS)), Mihaela Ifrim (University of Wisconsin-Madison), Igor Kukavica (University of Southern California), David Lannes (Institut de Mathématiques de Bordeaux; Centre National de la Recherche Scientifique (CNRS)), LEAD Daniel Tataru (University of California, Berkeley)
All scientific activities in this program will be available online so that those who can't attend in person are able to participate. If you are not a member of the program and would like to participate in any of the online activities, please fill out this REGISTRATION FORM.
PROGRAM DESCRIPTION
Fluid dynamics is one of the classical areas of partial differential equations, and has been the subject of extensive research over hundreds of years. It is perhaps one of the most challenging and exciting fields of scientific pursuit simply because of the complexity of the subject and the endless breadth of applications.
The focus of the program is on incompressible fluids, where water is a primary example. The fundamental equations in this area are the well-known Euler equations for inviscid fluids, and the Navier-Stokes equations for the viscous fluids. Relating the two is the problem of the zero viscosity limit, and its connection to the phenomena of turbulence. Water waves, or more generally interface problems in fluids, represent another target area for the program. Both theoretical and numerical aspects will be considered.
Updated on Oct 20, 2023 03:21 PM PDT -
Program Random and Arithmetic Structures in Topology -- Virtual Semester
Organizers: Nicolas Bergeron (École Normale Supérieure), Jeffrey Brock (Yale University), Alexander Furman (University of Illinois at Chicago), Tsachik Gelander (Weizmann Institute of Science), Ursula Hamenstädt (Rheinische Friedrich-Wilhelms-Universität Bonn), Fanny Kassel (Institut des Hautes Études Scientifiques (IHES)), LEAD Alan Reid (Rice University)
Until further notice, the MSRI building will only be open to a small group of essential staff and members of the Fall 2020 scientific programs.
All scientific activities in this program will be available online so that those who can't attend in person are able to participate. If you are not a member of the program and would like to participate in any of the online activities, please fill out this REGISTRATION FORM.
Updated on Sep 21, 2020 04:57 PM PDT
