-
Workshop Introductory Workshop: Topological and Geometric Structures in Low Dimensions & Geometry and Dynamics for Discrete Subgroups of Higher Rank Lie Groups
Organizers: Federica Fanoni (Université Paris-Est Créteil Val-de-Marne), Steven Frankel (Washington University), LEAD Yair Minsky (Yale University), Amir Mohammadi (University of California, Berkeley), Andrés Sambarino (Université de Paris VII (Denis Diderot) et Université de Paris VI (Pierre et Marie Curie)), Barbara Schapira (Université de Picardie (Jules Verne)), Genevieve Walsh (Tufts University)
The joint introductory workshop for the programs in Geometry and Dynamics for Discrete Subgroups of Higher Rank Lie Groups and Topological and Geometric Structures in Low Dimensions will feature lectures introducing subjects of interest to both programs, including Teichmuller Theory, geometry in higher rank, foliations and flows, Anosov groups and thermodynamic formalism, mapping class groups, counting and equidistribution, and related topics. Minicourses will be targeted at early career researchers as well as specialists looking to find connections between the different subjects.
Updated on Jan 07, 2026 11:04 AM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar GDLG Seminar: Topological Ax—Lindenmann Theorem
Updated on Jan 21, 2026 04:01 PM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar: Singularity of Cannon-Thurston maps
Updated on Jan 22, 2026 12:37 PM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:58 PM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
Seminar SSL Colloquium
Updated on Oct 27, 2025 10:21 AM PDT -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:59 PM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:59 PM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 04:00 PM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
Seminar SSL Colloquium
Updated on Oct 27, 2025 10:21 AM PDT -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
Workshop Recent Progress in Topological and Geometric Structures in Low Dimensions
Organizers: Kenneth Bromberg (University of Utah), Sergio Fenley (Florida State University), Autumn Kent (University of Wisconsin-Madison), LEAD Kathryn Mann (Cornell University), Kasra Rafi (University of Toronto)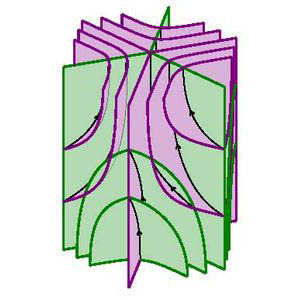 Foliations around a pseudo-Anosov singularity (Image credit: Chi Cheuk Tsang)
Foliations around a pseudo-Anosov singularity (Image credit: Chi Cheuk Tsang)This workshop will bring together ideas from diverse areas of mathematics that meet in the setting of geometry and topology in low dimensions. This includes the study of flows, foliations, and fibrations of three-manifolds and the related study of geometry (e.g. hyperbolic or conformal structures) of the manifolds and of the leaves or fibers, and their mapping class groups. This is a rich and interconnected area and many adjacent topics will also be featured.
Updated on Jan 07, 2026 11:05 AM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
Workshop Hot Topics: Geometric Langlands Conjecture
Organizers: Justin Campbell (Brandeis University), Charlotte Chan (University of Michigan), Lin Chen (Tsinghua University), Kevin Lin (University of Chicago), Sergey Lysenko (Université de Lorraine; Université de Lorraine), William Sawin (Princeton University)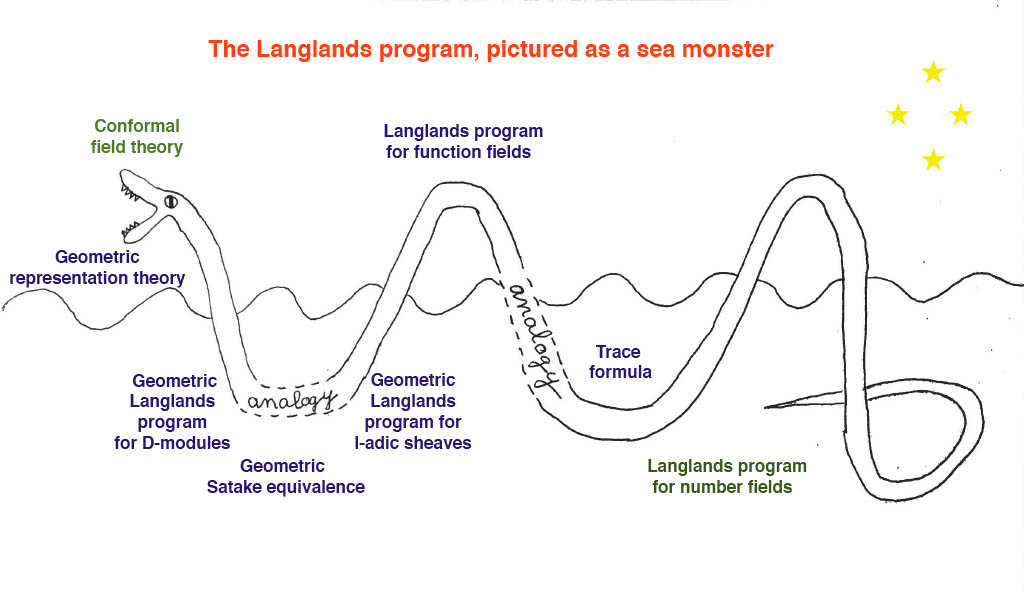 The Langlands program, pictured as a sea monster (Photo credit: V. Lafforgue)
The Langlands program, pictured as a sea monster (Photo credit: V. Lafforgue)This workshop will focus on the recent proof of the global unramified geometric Langlands conjecture as well as potential future developments in this field.
Updated on Jan 22, 2026 04:39 PM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
Seminar SSL Colloquium
Updated on Oct 27, 2025 10:22 AM PDT -
Workshop Homogeneous Dynamics and Anosov Representations
Organizers: Simion Filip (University of Chicago), Ursula Hamenstädt (Rheinische Friedrich-Wilhelms-Universität Bonn), LEAD Fanny Kassel (Institut des Hautes Études Scientifiques (IHES)), Hee Oh (Yale University), Jean-François Quint (CNRS - Université de Montpellier) Limit set of an Anosov representation
Limit set of an Anosov representationThis workshop will focus on recent advances on geometric and dynamical approaches to the study of discrete subgroups of higher rank Lie groups and their deformation spaces. The goal will be to present results and exchange ideas from different areas of mathematics, and we hope to create bonds between several different mathematical communities.
Updated on Jan 07, 2026 11:06 AM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
Workshop Critical Issues in Mathematics Education 2026: Math Literacy for 21st Century Citizenship - Part II
Organizers: Robert Berry (Indiana University), Josue Cordones (Bronx Collaborative High School), Megan Franke (University of California, Los Angeles), Maisie Gholson (University of Michigan), Courtney Ginsberg (Math for America), Mark Hoover (University of Michigan), Yvonne Lai (University of Nebraska), LEAD Maisha Moses (The Young People's Project), LEAD Benjamin Moynihan (The Algebra Project, Inc.), Aris Winger (Georgia Gwinnett College)Building on the vision Bob Moses set out in the 1993 Algebra Initiative Colloquium, the 2025 Critical Issues in Mathematics Education (CIME) Workshop celebrated the legacy of Moses’ call for a mathematics literacy that supports citizenship in the 21st century. A mathematics towards citizenship has proved elusive as a goal for mathematicians, mathematics educators, researchers, students, teachers, and leaders—even as efforts among different individuals, organizations, and communities labor for greater access to high-quality mathematics learning experiences. The 2026 CIME Workshop, Math Literacy for 21st Century Citizenship - Part II, endeavors to design opportunities for learning, collaborating, and struggling towards a mathematics for lived citizenship, as a theme and organizing principle for communities across the Nation.
For Moses, the notion of lived citizenship is not simply a matter of gaining legal status but of demanding that the legal status be meaningful. Thus mathematics literacy for lived or participatory citizenship might be thought of to include contributing to your community, not just being part of a community, and beyond belonging, to actively participate in making your community better, in making life better for others.
The conception of mathematics for lived citizenship is an important foundation for the goals for the 2026 CIME Workshop, in order to envision the development of coordinated actions in the short and long term within the mathematics and mathematics education communities. To ground and catalyze these efforts, we invite participants to consider a mathematics for lived citizenship through three foundational ideas:
- Claiming mathematics -- establishing agency in and ownership of math.
- Building Agency -- claiming and leveraging mathematics knowledge to overcome present day, generational, community, and national challenges.
- Collaboration and collective effort -- using mathematics literacy to make systemic change.
Three questions will guide our work:
- How does the unfolding history of mathematics impact lived citizenship?
- How do we understand the relationship between mathematical flourishing and the evolution of vibrant democracy in the United States?
- In light of the above two questions, how do we reimagine our roles, responsibilities, and actions in the short and long term?
Updated on Jan 07, 2026 11:06 AM PST -
Summer Graduate School Séminaire de Mathématiques Supérieures 2026: Universal Statistics in Number Theory (Montréal, Canada)
Organizers: Louis-Pierre Arguin (University of Oxford), Andrew Granville (Université de Montréal), Dimitris Koukoulopoulos (Université de Montréal), Matilde Lalin (Université de Montréal), Carlo Pagano (Concordia University), Elliott Paquette (McGill University), Frank Thorne (University of South Carolina)
One of the hottest topics in analytic number theory involves the use of statistics and probability in understanding different aspects of algebraic and analytic number theory, through various new lenses. This is reflected in some of the most exciting number theory research of the last few years (for example, of Bhargava, of Ellenberg and Venkatesh, of Alexander Smith, of Sawin and Wood, of Adam Harper, of Koukoulopoulos and Maynard, of Helfgott and Radziwill, of Pilatte,....). As a consequence the CRM will host a thematic semester Mar 2-July 3, 2026 on these topics involving some of the world leaders in the subject. Since this new area can roughly be split in two into Algebraic and Analytic, we will focus for two months on each, with the SMS school placed in the middle. The 2026 SMS will introduce junior mathematicians to important trends in number theory.
Updated on Oct 17, 2025 04:27 PM PDT -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
Seminar SSL Colloquium
Updated on Oct 27, 2025 10:23 AM PDT -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: 3-manifold seminar
Updated on Jan 22, 2026 12:28 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
Seminar GDLG Seminar
Updated on Jan 21, 2026 03:57 PM PST -
Seminar TGS: Topology Seminar
Updated on Jan 22, 2026 12:34 PM PST -
PROOF PROOF 2026
PROOF (Promoting Research Opportunities and Open Forums) is a two-week summer program designed to provide research opportunities for U.S.-based mathematicians, statisticians, and their collaborators in the U.S. and abroad, whose ongoing research may have been impacted by factors such as heavy teaching loads, professional isolation, limited access to funding, heavy administrative duties, personal obligations, or other constraints.
The program welcomes in-person participation from faculty and advanced graduate students at all U.S. colleges and universities. It aligns with SLMath’s broader goal to open doors to mathematics by creating environments where researchers from a wide range of institutional settings can thrive, pursue projects, and reach their full academic/scientific potential.
Updated on Nov 18, 2025 12:44 PM PST -
Summer Graduate School Percolation and Lattice Models of Statistical Physics (Columbia University)
Organizers: Roland Bauerschmidt (New York University, Courant Institute), Tom Hutchcroft (California Institute of Technology) <p>The five largest clusters in critical site percolation on a large three-dimensional box</p>
<p>The five largest clusters in critical site percolation on a large three-dimensional box</p>Percolation and spin models such as the Ising model have a history that goes back over 100 years. The subject has taken a central role in probability theory over the last few decades, in particular through interactions with various other areas of mathematics. These include graph theory, theoretical
computer science, statistical physics, quantum field theory, complex analysis, partial differential equations, and geometric group theory. Through examples, the summer school aims to illustrate some of the successful techniques and ideas in the subject area.Updated on Aug 26, 2025 12:45 PM PDT -
Summer Graduate School Geometric Measure Theory (SLMath)
Organizers: Camillo De Lellis (Institute for Advanced Study), Guido De Philippis (Hausdorff Research Institute for Mathematics, University of Bonn)
The school will consist of three interrelated courses, aimed to introduce the main concepts in Geometric Measure Theory.
(1) Sets and measure in the Euclidean space, Guido De Philippis (Courant Institute of Mathematical Sciences)
(2) Theory of currents, Annalisa Massaccesi (University of Padua)
(3) Allard regularity theory, Camillo De Lellis (Institute of Advanced Study)Updated on Sep 25, 2025 02:36 PM PDT -
MSRI-UP MSRI-UP 2026: Numerical Methods for Differential Equations
Organizers: LEAD Alexander Diaz-Lopez (Villanova University), Maria Mercedes Franco (Queensborough Community College (CUNY)), Rebecca Garcia (Colorado College), Johnny Guzman (Brown University), Candice Price (Smith College), Robin Wilson (Loyola Marymount University)The MSRI-UP summer program is designed to serve a diverse group of undergraduate students who would like to conduct research in the mathematical sciences.
In 2026, MSRI-UP will focus on Numerical Methods for Differential Equations The research program will be led by Dr. Johnny Guzman of Brown University.
Updated on Dec 17, 2025 04:12 PM PST -
Summer Graduate School ICTP-INdAM-SLMath School: Mathematics For Machine Learning (Trieste, Italy)
Organizers: Claudio Arezzo (Abdus Salam International Centre for Theoretical Physics), Jean Barbier (Abdus Salam International Centre for Theoretical Physics), Filippo Bracci (Università di Roma Tor Vergata), LEAD Domenico Marinucci (Università di Roma Tor Vergata), Cristina Trombetti (CSEF and Università degli Studi di Napoli Federico II)
The aim of this summer school is to provide an introduction to theoretical ideas that have been developed with the objective of understanding machine learning methods and their domain of applicability. The focus will be on proof technique and general mathematical tools. The lecturers are two worldwide experts in the area and the material is regularly taught in Mathematics and Statistics Departments of the top world Universities.
Updated on Jan 05, 2026 03:53 PM PST -
Summer Graduate School Random Growth Models, Phase Separation and Hamilton-Jacobi PDE (UC Berkeley)
Organizers: Alan Hammond (University of California, Berkeley), Fraydoun Rezakhanlou (University of California, Berkeley)Models of random growth and of the separation of phases occurring when one substance is suspended in another often evince universal features, in which scaling exponents are shared among a broad class of such models. A foothold for understanding such features is often offered by studying a few special models that are exactly solvable, which means that exact formulas of algebraic or integrable origin are available. Showing that a broader range of models also have the features is a task that may rely on a range of robust probabilistic or geometric tools. The summer school will offer an introduction to random growth and phase separation, with an emphasis on tools that offer the prospect of proving universality for a wider class of models.
Updated on Aug 26, 2025 02:14 PM PDT -
LATTICE LATTICE 2026
Lasting Alliance Through Team Immersion and Collaborative Exploration (LATTICE) is a yearlong program which provides opportunities for U.S. mathematicians to conduct collaborative research on topics at the forefront of the mathematical and statistical sciences. The goal of the program is to advance mathematical research by offering a structured environment where participants can concentrate on their work, make substantial progress, build professional connections, and contribute to the overall growth of the mathematical sciences. This program is designed for faculty whose research momentum may be affected by demanding teaching loads, limited access to research infrastructure, professional isolation, administrative responsibilities, or personal obligations.
Updated on Jan 12, 2026 04:07 PM PST -
Summer Graduate School John Tukey Summer Graduate School: Mathematics of Generative Models (SLMath)
Organizers: Jianfeng Lu (Duke University), Eric Vanden-Eijnden (New York University, Courant Institute) <p>Artificial image generation by flow-based generative models starting from noise</p>
<p>Artificial image generation by flow-based generative models starting from noise</p>The overarching goal of this summer school is to expose students to the latest developments in the mathematics of generative models. Our ultimate goal is to teach them how to conduct research in this exciting area in machine learning and use their knowledge to make contributions to applied mathematics using these new tools.
Updated on Nov 06, 2025 09:24 AM PST -
Summer Graduate School SLMath-Oxford-OIST School: Analysis of Partial Differential Equations (Okinawa, Japan)
Organizers: Ugur Abdulla (Okinawa Institute of Science and Technology), Gui-Qiang Chen (University of Oxford)
This two week summer school, jointly organized by SLMath with OIST, will offer the following two mini-courses:
- Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
This course will present some recent developments in the theory of divergence-measure fields via measure-theoretic analysis and its applications to the analysis of nonlinear PDEs of conservative form – nonlinear conservation laws. - Perron’s method and Wiener-type criteria in the potential theory of elliptic and parabolic PDEs
This course will present some recent developments precisely characterizing the regularity of the point at ∞ for second order elliptic and parabolic PDEs and broadly extending the role of the Wiener test in classical analysis.
Updated on Dec 03, 2025 10:44 AM PST - Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
-
Summer Graduate School Dynamical Systems for Machine Learning and AI (IBM Yorktown)
Organizers: Haoyang Cao (Johns Hopkins University), Soumyadip Ghosh (IBM Thomas J. Watson Research Center), LEAD Yingdong Lu (IBM Thomas J. Watson Research Center), Tomasz Nowicki (IBM Thomas J. Watson Research Center), Yunan Yang (Cornell University)
This Summer Graduate School aims to introducing graduate students to some aspects of contemporary modeling and analysis of dynamical systems in their interactions with machine learning and artificial intelligence (AI) applications.
Updated on Aug 21, 2025 12:08 PM PDT -
Summer Graduate School Singularities in Commutative Algebra Through Cohomological Methods (SLMath)
Organizers: Benjamin Briggs (Imperial College, London), Eloísa Grifo (University of Nebraska), Josh Pollitz (Syracuse University) <p>Homotopy measures how spheres can be tangled in spaces; the logo shows a sphere tangled in a grove of California redwoods<br />The background painting is “Giant Redwood Trees of California” by Albert Bierstadt in 1874</p>
<p>Homotopy measures how spheres can be tangled in spaces; the logo shows a sphere tangled in a grove of California redwoods<br />The background painting is “Giant Redwood Trees of California” by Albert Bierstadt in 1874</p>The goal of this school will be to introduce students to several powerful cohomological tools that were brought to commutative algebra by Avramov in the 80s and 90s: Lie algebra methods from homotopy theory, and support theoretic methods from the representation theory of finite groups. These tools have have seen a huge array of applications that continue to grow, with several major developments in recent years, opening new connections to algebraic topology, noncommutative algebraic geometry, and representation theory.
Updated on Oct 03, 2025 10:23 AM PDT -
Summer Graduate School Moduli of Varieties (SLMath)
Organizers: Kenneth Ascher (University of California, Irvine), Dori Bejleri (University of Maryland), Kristin DeVleming (University of California, San Diego)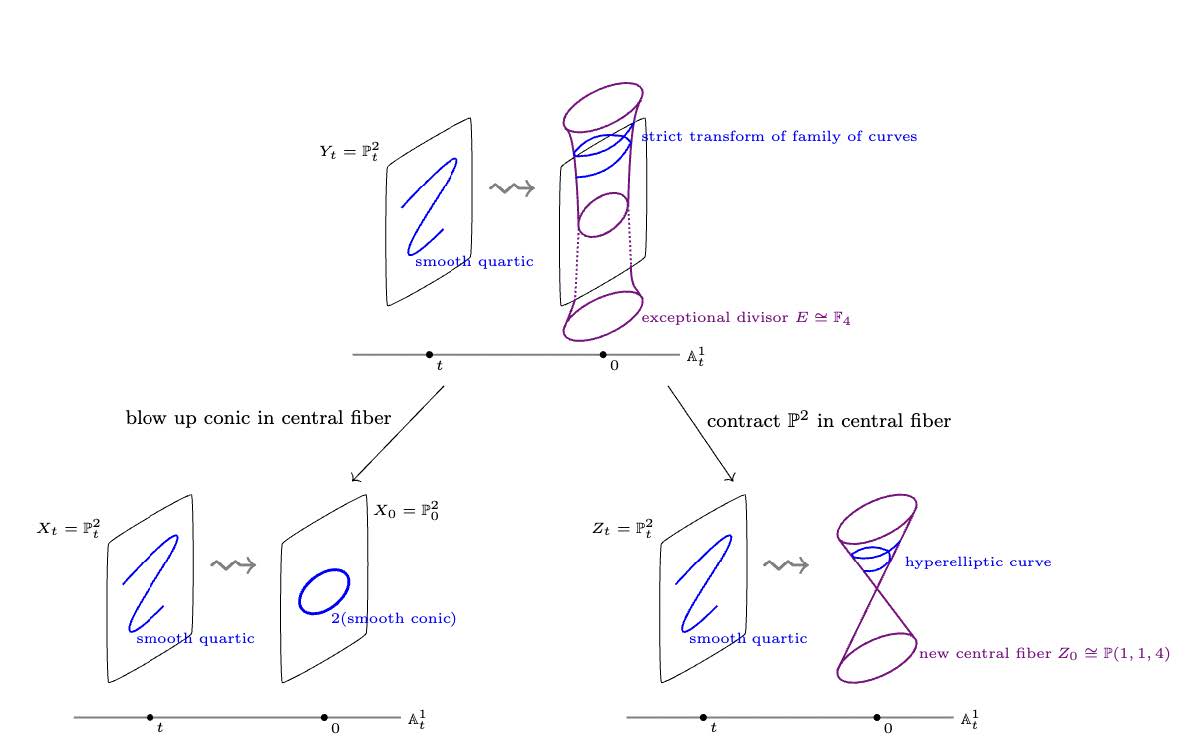 <p>A wall-crossing in a moduli problem</p>
<p>A wall-crossing in a moduli problem</p>One of the central problems in algebraic geometry is to classify so-called algebraic varieties: geometric shapes cut out by polynomial equations. Algebraic varieties are parametrized by certain moduli spaces (roughly: parameter spaces whose points correspond to these different varieties). The geometry of these moduli spaces encodes the ways of continuously deforming these shapes. Furthermore, classification questions for algebraic varieties often boil down to understanding the geometry of these moduli spaces. In the past few years, powerful new tools have been developed in moduli theory, especially for higher dimensional varieties – those which are of complex dimension at least two. The goal of this summer school is to provide an introduction to many of these recently emerging breakthroughs to enable graduate students to begin working in this area. The program will be motivated and often guided by examples and is intended to be accessible to a wide variety of students
Updated on Oct 07, 2025 09:46 AM PDT -
Program Representation Theory Under the Influence of Quantum Field Theory
Organizers: David Ben-Zvi (University of Texas, Austin), LEAD Tudor Dimofte (University of Edinburgh), Iva Halacheva (Northeastern University), LEAD Joel Kamnitzer (McGill University), Pavel Safronov (University of Edinburgh), Peng Shan (Tsinghua University) <p>Illustrated by Rok Gregoric</p>
<p>Illustrated by Rok Gregoric</p>The upcoming SLMath program is organized around key themes of “higher” quantization and mirror symmetry as they impact and elucidate a wide variety of questions in representation theory. The program will bring together experts and young researchers from algebra, geometry, physics and number theory to help develop and disseminate this unified vision of a rapidly evolving field, exploring the mathematical consequences of the examples, structures, and dualities discovered in physics.
Updated on Jul 16, 2025 09:07 AM PDT -
Program Motivic Homotopy Theory: Connections and Applications
Organizers: LEAD Aravind Asok (University of Southern California), Adrien Dubouloz (Universit'e de Poitiers), Elden Elmanto (University of Toronto, Scarborough), Dan Isaksen (Wayne State University), Paul Oestvær (Universita degli studi Milano), Anand Sawant (Tata Institute of Fundamental Research), Kirsten Wickelgren (Duke University), Maria Yakerson (Institut de Mathématiques de Jussieu)Tremendous progress has been made using motivic techniques in geometric questions for affine algebraic varieties, especially those involving algebraic vector bundles. Computations in classical algebraic topology have been improved by motivic techniques, e.g., related to the problem of computing homotopy groups of spheres. Moreover, the theory has identified new structures of interest in arithmetic situations. Transformative recent progress in motivic homotopy theory has only broadened the scope for potential applications of motivic techniques, as well as new avenues of interaction with other areas of mathematics. This program will build on previous successes, explaining the tools that have been developed and how to use them, analyzing questions of the sort described above and identifying new domains where motivic techniques will be successful.
Updated on Jul 16, 2025 09:24 AM PDT -
Program Complementary Program Fall 2026
The Complementary Program has a limited number of memberships that are open to mathematicians whose interests are not closely related to the core programs; special consideration is given to mathematicians who are partners of an invited member of a core program.
Updated on Jan 15, 2026 03:02 PM PST -
Workshop Pathways Workshop: Representation Theory Under the Influence of Quantum Field Theory & Motivic Homotopy Theory
Organizers: Ana Balibanu (Louisiana State University), Asilata Bapat (Australian National University), Teena Gerhardt (Michigan State University), Iva Halacheva (Northeastern University), Padmavathi Srinivasan (Boston University), Kirsten Wickelgren (Duke University)Updated on Jun 10, 2025 11:08 AM PDT -
Workshop Introductory Workshop: Representation Theory Under the Influence of Quantum Field Theory & Motivic Homotopy Theory
Organizers: David Ben-Zvi (University of Texas, Austin), Elden Elmanto (University of Toronto, Scarborough), Iva Halacheva (Northeastern University), Pavel Safronov (University of Edinburgh), Anand Sawant (Tata Institute of Fundamental Research), Peng Shan (Tsinghua University), Craig Westerland (University of Minnesota Twin Cities), Maria Yakerson (Institut de Mathématiques de Jussieu)Updated on Jun 10, 2025 11:07 AM PDT -
Workshop Geometric Representation Theory and 3d Mirror Symmetry
Organizers: Tudor Dimofte (University of Edinburgh), Joel Kamnitzer (McGill University), Sam Raskin (University of Texas, Austin), Peng Shan (Tsinghua University), LEAD Benjamin Webster (University of Waterloo) Image by Elliot Kienzle
Image by Elliot KienzleThis workshop will bring together theoretical physicists, representation theorists, algebraic geometers and symplectic geometers interested the connections between quantum field theory and geometric representation theory. The main topics to be discussed are mathematical aspects of 2d, 3d and 4d supersymmetric field theories, such as: topological twists and the resulting Higgs and Coulomb branches, relations to quantization and categorification, representations of vertex operator algebras, connections to enumerative geometry and quantum K-theory and elliptic cohomology, relations to knot homology and, finally, connections to the (relative) geometric Langlands program.
Updated on Jul 15, 2025 04:27 PM PDT -
Workshop Motivic homotopy theory: connections and applications
Organizers: Adrien Dubouloz (Universit'e de Poitiers), LEAD Dan Isaksen (Wayne State University), Sabrina Pauli (Technische Universitat Darmstadt)The workshop will bring together researchers at the forefront of ongoing work in motivic homotopy theory. Topics will include the application of motivic techniques to: geometry of affine algebraic varieties and algebraic vector bundles; computations in classical algebraic topology such as homotopy groups of spheres; and enumerative geometry. The workshop will also consider the internal foundational development of motivic homotopy theory itself.
Created on Oct 09, 2025 10:20 AM PDT -
AxIOM Commutative Algebra, Representation Theory, and Other Interactions
Organizers: LEAD David Eisenbud (University of California, Berkeley), Srikanth Iyengar (University of Utah), Claudia Polini (University of Notre Dame), Bernd Ulrich (Purdue University) <p> </p><p>A line and a twisted cubic form the complete intersection of two quadric surfaces (shown in red and yellow). This is the simplest interesting example of the relation of linkage.</p>
<p> </p><p>A line and a twisted cubic form the complete intersection of two quadric surfaces (shown in red and yellow). This is the simplest interesting example of the relation of linkage.</p>The AxIOM seeks to build on the many interactions between commutative algebra, representation theory and other areas of mathematics. The focus will be new developments in these subjects, many inspried by the 2024 Commutative Algebra program. Some of the major themes to be covered are linkage theory, syzygies, and new interactions between commutative algebra and algebraic number theory.
Updated on Jan 16, 2026 03:00 PM PST -
AxIOM Building the Mathematical Library of the Future
Organizers: LEAD Kevin Buzzard (Imperial College, London), Jireh Loreaux (Southern Illinois University), Emily Riehl (Johns Hopkins University), Adam Topaz (University of Alberta)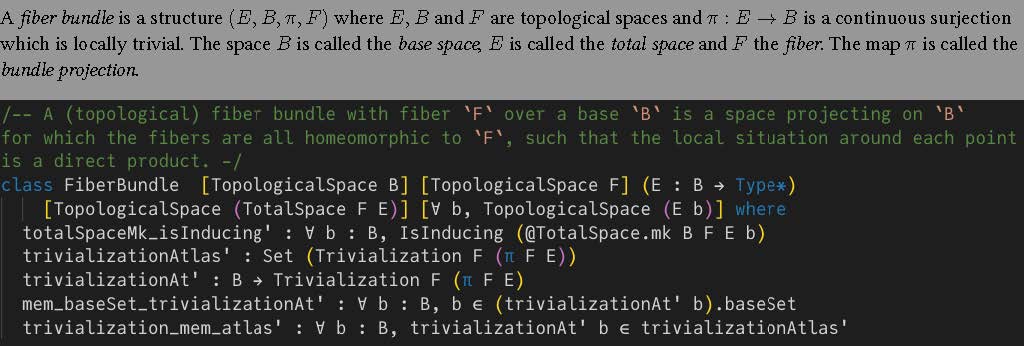 <p>Formalization of the definition of a fiber bundle in Lean, from the Mathlib library</p>
<p>Formalization of the definition of a fiber bundle in Lean, from the Mathlib library</p>A challenging aspect of computer formalization is formalizing definitions that are (i) mathematically correct (something that is not automatically verifiable and must be checked by human experts), (ii) optimized for usability and (iii) at the appropriate level of generality. The AxIOM "Building the mathematical library of the future" will focus on formalizing definitions in Lean across a wide range of mathematical subject areas in the hope that it will be possible to correctly formalize the statements of recent theorems from the research literature. Such work is essential for making formal verification tools more relevant to mathematics researchers.
Updated on Jan 16, 2026 10:44 AM PST -
Program New Trends in Tropical Geometry
Organizers: Pierrick Bousseau (University of Georgia), Melody Chan (Brown University), Ilia Itenberg (Institut de Mathématiques de Jussieu - Paris Rive Gauche), Hannah Markwig (Eberhard-Karls-Universität Tübingen), LEAD Kris Shaw (University of Oslo) Tropical surfaces. Images courtesy of Lars Allermann.
Tropical surfaces. Images courtesy of Lars Allermann.Tropical geometry can be viewed as a degenerate version of algebraic geometry,where the role of algebraic varieties is played by certain polyhedral complexes. As the degeneration process, called tropicalization, preserves many fundamental properties, tropical geometry provides important bridges and an exchange of methods between algebraic geometry, symplectic geometry and convex geometry; these links have been extremely fruitful and gave rise to remarkable results during the last 20 years. The main focus of the program will be on the most significant recent developments in tropical geometry and its applications. The following topics are particularly influential in the area and will be central in the program:
- real aspects of tropical geometry;
- tropical mirror symmetry and non-Archimedean geometry;
- tropical phenomena in symplectic geometry;
- matroids, combinatorial and algebraic aspects;
- tropical moduli spaces;
- tropical geometry and A1-homotopy theory.
Updated on Jul 10, 2025 09:28 AM PDT -
Program Algebraic Combinatorics
Organizers: Sara Billey (University of Washington), LEAD Sylvie Corteel (Université de Paris VII (Denis Diderot); University of California, Berkeley), Philippe Di Francesco (University of Illinois at Urbana-Champaign), Cynthia Vinzant (University of Washington), Lauren Williams (Harvard University) Picture of an amplituhedron
Picture of an amplituhedronAlgebraic combinatorics is an area of mathematics that employs methods in abstract algebra in combinatorial contexts, and that uses combinatorial methods to approach problems in algebra. Some important topics are symmetric functions, Young tableaux, matroids, Coxeter combinatorics. There are links to computer algebra (sage-combinat), number theory (L-functions), representation theory, and mathematical physics through Macdonald processes and integrability. The work on the totally positive Grassmannian also gave rise to beautiful results in mathematical physics: for example KP solitons and Scattering Amplitudes. Schubert calculus is an important part of algebraic combinatorics and is now at the frontier with k-Schur functions, which first came up in the theory of Macdonald polynomials.
Updated on Jul 10, 2025 09:39 AM PDT -
Workshop Pathways Workshop: Algebraic Combinatorics & New Trends in Tropical Geometry
Organizers: Renzo Cavalieri (Colorado State University), Sylvie Corteel (Université de Paris VII (Denis Diderot); University of California, Berkeley), Olya Mandelshtam (University of Waterloo), LEAD Hannah Markwig (Eberhard-Karls-Universität Tübingen), Sarah Mason (Wake Forest University), Kris Shaw (University of Oslo)
This workshop presents introductory talks and new trends in tropical geometry and algebraic combinatorics, including interactions between tropical geometry and enumerative, logarithmic, nonarchimedean, and real algebraic geometry, mirror symmetry and symplectic geometry, moduli spaces in tropical geometry, the geometry of matroids, integrable systems and dynamical combinatorics, combinatorial representation theory, geometry of polynomials, combinatorial varieties and connections to symmetric function theory and cluster algebras.
Updated on Nov 13, 2025 12:23 PM PST -
Workshop Introductory Workshop: Algebraic Combinatorics & New Trends in Tropical Geometry
Organizers: Philippe Di Francesco (University of Illinois at Urbana-Champaign), LEAD Ilia Itenberg (Institut de Mathématiques de Jussieu - Paris Rive Gauche), Svante Linusson (Royal Institute of Technology), Sam Payne (University of Texas, Austin), LEAD Colleen Robichaux (University of California, Los Angeles), Kris Shaw (University of Oslo), Lauren Williams (Harvard University), Josephine Yu (Georgia Institute of Technology)
The workshop will include three minicourses on key topics in Algebraic Combinatorics & Tropical Geometry: combinatorial representation theory, combinatorial algebraic varieties and their connections to various polynomial bases, combinatorial and algebro-geometric facets of matroids, enumerative tropical geometry, real aspects of tropical geometry and connections with A1-homotopy theory.
The minicourses will be intended for a broad audience, with the goal of providing background and motivation in these topics.Updated on Jan 16, 2026 04:30 PM PST -
Program Inverse Problems and Applications
Organizers: Fioralba Cakoni (Rutgers University), Maarten de Hoop (Rice University), Anna Gilbert (Yale University), Katya Krupchyk (University of California, Irvine), Matti Lassas (University of Helsinki), LEAD Gunther Uhlmann (University of Washington)
Inverse problems (IP) arise in all fields of science and technology where a cause for an observed or desired effect is sought. In the last 50 years or so there has been substantial progress in the mathematical understanding of these problems but many questions remain open. The mathematics of these problems involves many areas in Mathematics including PDE, differential geometry, integral geometry, probability, statistics, complex analysis, numerical analysis, mathematical physics, data science, etc. Since the 2010 program at the then-Mathematical Sciences Research Institute (now Simons Laufer Mathematical Sciences Institute), there has been significant progress in inverse problems; many of the advances can be traced back to that program. However, there are still deep open questions remaining as well, some of which are discussed in this proposal. New research topics include the connection between IP and machine learning, IP for nonlinear equations, IP for nonlocal operators, and connections between statistics and IP.
Updated on Nov 06, 2025 12:15 PM PST -
Program Geometric Measure Theory
Organizers: Otis Chodosh (Stanford University), Camillo De Lellis (Institute for Advanced Study), LEAD Guido De Philippis (Hausdorff Research Institute for Mathematics, University of Bonn), Svitlana Mayboroda (University of Minnesota, Twin Cities), Robin Neumayer (Northwestern University), Luca Spolaor (University of California, San Diego), Zihui Zhao (Johns Hopkins University)
The field of Geoemtric Measure Theory (GMT)has become vast and many gaps between disparate areas have emerged. This thematic semester will bring together researchers from every corner of the field, to kick-start new interactions and discoveries. In light of the many exciting advancements and potential for future breakthroughs, this as a crucial moment to bring old and new members of the GMT community together. The program will encourage interactions between established experts, emerging researchers and students, allowing for the sharing of key idea that brought to the recent developments and helping to shape a research agenda for the future.
Updated on Jul 10, 2025 09:27 AM PDT -
Program Hodge Theory
Organizers: Ben Bakker (University of Illinois, Chicago), Robert Friedman (Columbia University), LEAD Radu Laza (State University of New York, Stony Brook), Colleen Robles (Duke University), Christian Schnell (State University of New York, Stony Brook), Junliang Shen (Yale University), Qizheng Yin (Fudan University) Stylized Hodge diamond
Stylized Hodge diamondHodge theory originated in the work of Hodge, Kodaira, and Weyl, who introduced analytic methods, particularly techniques from partial differential equations, to study the cohomology of compact Riemannian manifolds. Since then, Hodge theory has developed into a central and unifying framework in both complex and algebraic geometry. It plays a fundamental role in the study of algebraic cycles and moduli spaces, and it has deep connections with many other areas of mathematics, including model theory, symplectic geometry, singularity theory, D-modules and perverse sheaves, derived categories, representation theory, as well as arithmetic geometry and number theory. Over the past two decades, the field has witnessed remarkable progress, driven by the interaction of Hodge theory with tools and ideas from diverse areas.
Updated on Jan 20, 2026 11:37 AM PST -
Program Geometry and Combinatorics of Artin Groups and Arrangements
Organizers: Daniel Allcock (University of Texas, Austin), Christin Bibby (Louisiana State University), Ruth Charney (Brandeis University), Emanuele Delucchi (University of Applied Arts and Sciences of Southern Switzerland), Jon McCammond (University of California, Santa Barbara), LEAD Giovanni Paolini (Università di Bologna), Mario Salvetti (Università di Pisa)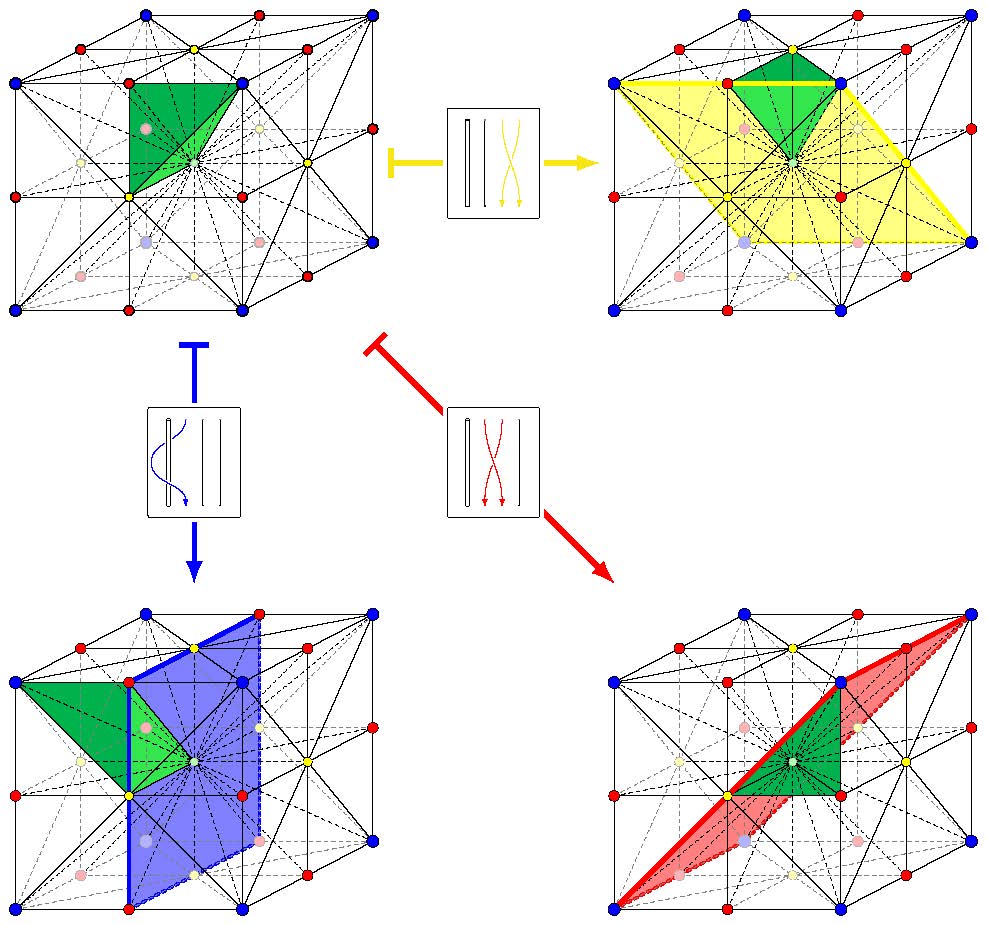 <p>Generators and their reflecting hyperplanes for the B3 Artin group</p>
<p>Generators and their reflecting hyperplanes for the B3 Artin group</p>Artin groups and arrangements are closely connected research areas at the crossroads of algebra, geometry and combinatorics. Recent progress on classical problems and the development of new techniques has led to intense activity both internally and in connection with adjacent research areas. Our program will build upon recent breakthroughs, address foundational questions and foster exchange between experts. We aim at strengthening the emerging connections with other research areas and encouraging junior researchers to engage with this broader landscape.
Updated on Jan 20, 2026 11:28 AM PST
|
|
Upcoming Scientific Events |