The African Diaspora Joint Mathematics Workshop (ADJOINT) is a yearlong program that provides opportunities for U.S. mathematicians – especially those from the African Diaspora – to form collaborations with distinguished African-American research leaders on topics at the forefront of mathematical and statistical research.
Beginning with an intensive two-week summer session at MSRI, participants work in small groups under the guidance of some of the nation’s foremost mathematicians and statisticians to expand their research portfolios into new areas. Throughout the following academic year, the program provides conference and travel support to increase opportunities for collaboration, maximize researcher visibility, and engender a sense of community among participants. The 2022 program takes place June 20 - July 1, 2022 in Berkeley, California.
ADJOINT enriches the mathematical and statistical sciences as a whole by providing a platform for African-American mathematicians to advance their research and careers and deepen their engagement with the broader research community.
The ADJOINT 2022 workshop is now concluded.
To receive announcements, sign up for our newsletter or follow @mathmoves on Twitter.
About the Program
Each summer, three to five research leaders will each propose a research topic to be studied during a two-week workshop.
During the workshop, each participant will:
- conduct research at MSRI within a group of four to five mathematical and statistical scientists under the direction of one of the research leaders
- participate in professional enhancement activities provided by the onsite ADJOINT Director
- receive funding for two weeks of lodging, meals and incidentals, and one round-trip travel to Berkeley, CA
After the two-week workshop, each participant will:
- have the opportunity to further their research project with the team members including the research leader
- have access to funding (up to $2000 per person) to attend conference(s) or to meet with other team members to pursue the research project, or to present results
- become part of a network of research and career mentors.
The 2022 ADJOINT Program Director is Dr. Caleb Ashley (Boston College).
Learn more about the ADJOINT experience in this video interview:
Eligibility
Applicants must be a U.S. citizen or permanent resident, possess a Ph.D. in the mathematical or statistical sciences, and be employed at a U.S. institution.
Selection Process
The guiding principle in selecting participants and establishing the groups is the creation of diverse teams whose members come from a variety of institutional types and career stages. The degree of potential positive impact on the careers of African-Americans in the mathematical and statistical sciences will be an important factor in the final decisions.
ADJOINT 2022 Application Process and Deadline
The ADJOINT 2022 workshop takes place at MSRI in Berkeley, California from June 20 - July 1, 2022. The research leaders and research topics can be found below.
Applications for ADJOINT 2022 may be submitted via MathPrograms beginning August 15, 2021.
- a cover letter specifying which of the offered research projects you wish to be part of; if more than one please indicate your priorities
- a CV
- a personal statement, no longer than one page, addressing how your participation will contribute to the goals of the program (e.g., why you are a good candidate for this workshop and what you hope to gain)
- a research statement, no longer than two pages, describing your current research interests, and relevant past research activities, and how they relate to the project(s) of greatest interest to you (e.g., what motivates your current interests and what is your relevant research background)
Due to funding restrictions, only U.S. citizens and permanent residents are eligible to apply.
For more information, please contact Christine Marshall, MSRI's Program Manager at coord@msri.org.
2022 Research Leaders and Topics
Rebecca Hubbard (Perelman School of Medicine, University of Pennsylvania)
"Improving validity and fairness of EHR research for medically underserved populations"
Healthcare-derived data including data from electronic health records (EHR) and medical claims have emerged as a key resource for learning about the health of populations and impact of medical interventions. Although healthcare-derived data are now widely used in biomedical studies, these data sources have many deficiencies including complex patterns of missingness and measurement error. For example, in contrast to data collected for research, healthcare data are generated when a patient seeks care in the healthcare system. As a result, the specific data elements available for a given patient vary in direct relation to the extent of the patient’s healthcare involvement. An important consequence of this differential EHR data availability is its impact on the validity of research conducted in medically underserved populations. Patients who receive less or poorer quality care, including racial and ethnic minority and socioeconomically vulnerable populations, also have poorer quality data. Research using healthcare-derived data thus may generate results with poorer statistical properties for underserved populations and potentially exacerbate health disparities.
In this project, using healthcare-derived data and statistical simulation studies, we will investigate variability in data quality across underserved populations, quantify the impact of this differential data quality on bias and precision of results, and investigate alternative statistical methods for bias reduction to improve the quality, generalizability and fairness of research using healthcare-derived data.
Trachette L. Jackson (University of Michigan)
"Mathematical Model of Targeted Cancer Therapeutics"
Mathematical and computational modeling approaches have been applied to every aspect of cancer biology, from tumor initiation to malignant spread and treatment response. To pinpoint specific pathways critical for tumor progression, a substantial amount of research aimed at improving therapeutic outcomes for cancers is now focusing on the molecular biology of individual tumors. Increased understanding of these molecular mechanisms that mediate cancer pathogenesis is leading to the targeted manipulation of these pathways and the development of new cell-specific approaches to cancer therapy.
A powerful and practical way to optimize novel drug combinations for clinical cancer treatment is to use data-driven mathematical models. The overarching goal of this project is to develop such models of promising targeted cancer therapeutic agents that account for the variability in mechanistic processes associated with cell decision-making. We will leverage this heterogeneity to set up a virtual cohort of patients and run treatment optimization studies to predict treatment combinations that minimize tumor burden and/or maximize survival. We anticipate that this will allow us to identify attributes characterizing subpopulations that benefit most /least from these interventions alone and in combination with more traditional therapeutic approaches.
Gaston M. N'Guerekata (Morgan State University)
"Fractional Calculus and Applications to Finance and Biology"
Fractional Calculus is a three century old topic. Its study goes back to Leibniz, the inventor of the notation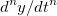 
for positive integral n as the derivatives of a function y. In a 1965 correspondence, L’Hospital wrote to Leibniz: ”What if n = 1/2?”. Leibniz responded: ”This is an apparent paradox from which, one day, useful consequences will be drawn.” Indeed, a long line of mathematicians were inspired by this question. Some early contributors to the study of fractional calculus include Euler (1730), Lagrange (1772), Fourier (1822), Liouville (1832), Riemann (1847), Leitnikov (1868), Laurent (1884), Krug (1890), and Weyl (1917).
Over the last decade, there has been a resurgence of study of fractional differential equations and their applications. Fractional differential equations are more appropriate and more efficient in modeling of memory-dependent phenomena as well as modeling in complex media, such as porous ones. For example, the fractional derivative of a financial process at a specific time is effected by all of the information and behavior of the model in all previous moments. In comparison, the classical derivative at a specific time is affected only by the information in the local neighborhood of that time. Surprisingly, a fractional order system is more stable than its integer model since the stability domain in the complex space of eigenvalues of the linearized system for fractional differential equations remains contained and is larger than the corresponding domain for ordinary differential equations.
In this research project, we will introduce some basic and popular concepts of derivatives of fractional order. We will review some applications to fractional modeling of financial and biological systems from recent literature. We will also propose the study of the existence, uniqueness, stability and long term behavior of mild solutions to some fractional evolution equations, both with and without impulses as research projects leading to publications.
ADJOINT Program Directors
- Dr. Edray Goins, Pomona College
- Dr. Caleb Ashley, Boston College (2022 site director)
- Dr. Naiomi Cameron, Spelman College
- Dr. Jacqueline Hughes-Oliver, North Carolina State University
- Dr. Anisah Nu’Man, Spelman College
Previous Years
MSRI has been supported from its origins by the National Science Foundation, now joined by the National Security Agency, over 100 Academic Sponsor departments, by a range of private foundations, and by generous and farsighted individuals. ADJOINT 2022 receives additional support from the Alfred P. Sloan Foundation.