In recent years techniques from harmonic analysis viz. projection theorems have found striking applications in finitary analysis on homogenous spaces. Such quantitative results have many potential applications to analytic number theory. This workshop will bring together researchers in these areas to further explore these connections.

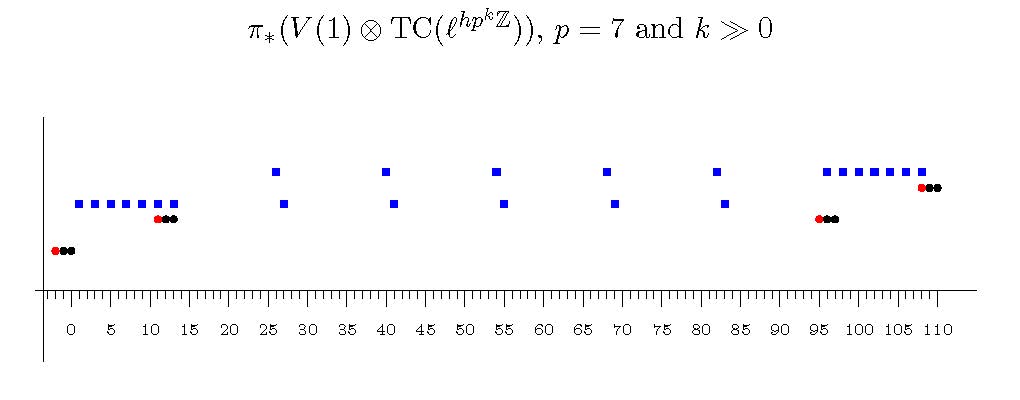
In June 2023, Burklund, Hahn, Levy, and Schlank surprised the homotopy theory community when they announced a disproof of Ravenel's Telescope Conjecture, a fundamental problem of homotopy theory which had been open for 40 years and was believed to be out of reach. The disproof of the Telescope Conjecture combines some of the most exciting recent developments in homotopy theory. This includes fundamental work on red-shift phenomena and descent in algebraic K-theory, trace methods based on a novel approach to topological Hochschild and cyclic homology, ambidexterity in chromatic homotopy theory, and more.

The workshop will explore this amazing body of work, culminating in its synthesis and ingenious application to disprove the Telescope Conjecture.

The affine line arrangement of type C with different lattices and toric arrangements arising from it.

This workshop brings together experts from different areas to discuss and foster collaboration on several topics of current interest related to Artin groups such as the K(π, 1) conjecture, hyperplane arrangements and abelian arrangements, combinatorial structures associated with dual Coxeter systems, and complexes of nonpositive curvature.

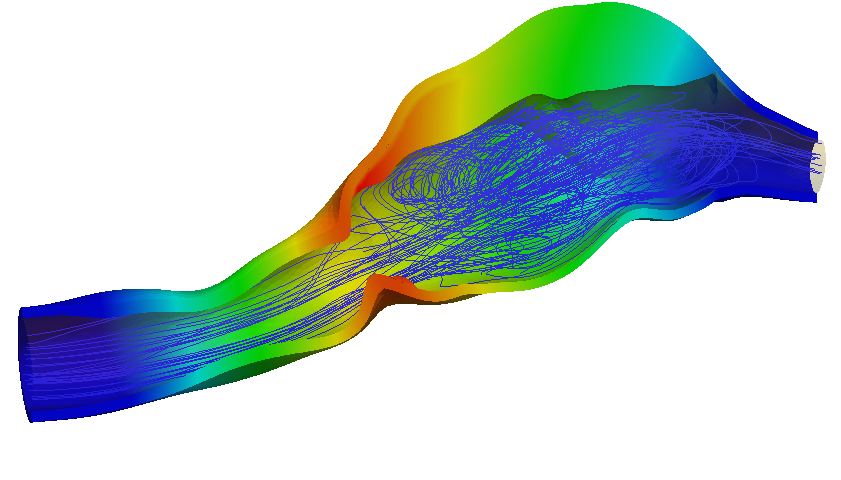Blood flow and structure displacement in an Aortic Abdominal Aneurysm

This workshop will focus on the coupled dynamical interaction between fluids and elastic/poroelastic structures, with an emphasis on the most recent and cutting-edge mathematical advances in deterministic and stochastic fluid-structure interaction. The goal of this workshop is to bring together a diverse group of mathematicians in the fields of analysis, modeling, numerics, stochastics, and real-world applications in order to showcase an interdisciplinary approach to the study of coupled fluid-structure systems. A major component of this workshop will be to encourage active participation of early career researchers, such as graduate students and postdocs, and foster synergistic collaboration with established leaders in the field.

Drawing by Tina Zhang.

This workshop is about the recent MIP*=RE result from quantum computational complexity, and the resulting resolution of the Connes embedding problem from the theory of von Neumann algebras. MIP*=RE connects the disparate areas of computational complexity theory, quantum information, operator algebras, and approximate representation theory. The aim of this workshop is to bridge this divide, by giving an in-depth exposition of the techniques used in the proof of MIP*=RE, and highlighting perspectives on the MIP*=RE result from operator algebras and approximate representation theory. In particular, this workshop will highlight connections with group stability, something that has not been covered in previous workshops. In addition to increasing understanding of the MIP*=RE proof, we hope that this will open up further applications of the ideas behind MIP*=RE in operator algebras.

This workshop will explore connections between the regularity theory of minimal surfaces and of mean curvature flow. Recent breakthroughs have improved our understanding of singularity formation in both settings but the current research trends are becoming increasingly disparate. Experts from both areas will present their research and there will be ample free time to establish connections between the topics.

When data automatically drop from the sky: intelligent approaches in data science change the way humans and computers interact. (Illustration: Niklas Briner)

Despite the remarkable success in extracting information from complex and (often) large-scale datasets over the last two decades, further progress is needed to making automated statistical and machine learning algorithms more reliable, robust, interpretable and trustworthy. This workshop has its focus on foundational aspects of this goal, linking areas at the interface between statistics, optimization, machine learning and computer science, such as distributional robustness and stability, adversarial and transfer learning, generalizability and meta analysis, and causality.

Image created by Nicolas Antille, of the visualization team of the Blue Brain Project at EPFL

This workshop will be held online May 4-7 and May 10-11, 2021. The Zoom link will be provided at a later time. You must register for the workshop to receive the password.  The workshop is held in Pacific Daylight Time.

The talks in this workshop will present a wide array of current applications of topology in neuroscience, including classification and synthesis of neuron morphologies, analysis of synaptic plasticity, algebraic analysis of the neural code, topological analysis of neural networks and their dynamics, topological decoding of neural activity, diagnosis of traumatic brain injuries, and topological biomarkers for psychiatric disease. Some of the talks will be devoted to promising new directions in algebraic topology that have been inspired by neuroscience.

Image drawn by Dr. Katy Craig

This workshop will be held online.  The link to join is: https://msri.zoom.us/j/92457794010. You must register for the workshop to receive the password.  The workshop is held in Pacific Standard Time.

Workshop Description:
The goal of the workshop is to explore the many emerging connections between the theory of Optimal Transport and models and algorithms currently used in the Machine Learning community. In particular, the use of Wasserstein metrics and the relation between discrete models and their continuous counterparts will be presented and discussed.

The purpose of the workshop is to explain Vincent Lafforgue's ground breaking work, constructing the automorphic to Galois direction of the Langlands correspondence for function fields. There will also be a number of talks on more recent developments and related results.

Tangled honeycomb networks | and the Advanced Light Source at LBNL

The fascinating and complicated microstructures of materials that are now visible through advanced imaging techniques challenge the frontiers of characterisation and understanding. At the same time, developments in modern geometric and topological techniques are beginning to illuminate important features of material structures, while the microstructures themselves and the analysis and prediction of their macroscopic properties are inspiring new directions in pure and applied mathematics. In a collaboration with the Lawrence Berkeley National Laboratory (LBNL), this workshop aims at intensifying the interaction of mathematicians with material scientists, physicists and chemists on the structural description and design of materials.

The homological conjectures in commutative algebra are a network of conjectures that have generated a tremendous amount of activity in the last 50 years. They had largely been resolved for commutative rings that contain a field, but, with the exception of some low dimensional cases, several remained open in mixed characteristic --- until recently, when Yves André announced a proof of Hochster's Direct Summand Conjecture. The progress comes from systematically applying Scholze's theory of perfectoid spaces, which had already shown its value by solving formidable problems in number theory and representation theory. One of the goals of the workshop is to cover the ingredients going into the proofs of the Direct Summand Conjecture.

Cluster algebras were introduced in 2001 by Fomin and Zelevinsky to capture the combinatorics of canonical bases and total positivity in semisimple Lie groups. Since then they have revealed a rich combinatorial and group-theoretic structure, and have had significant impact beyond these initial subjects, including string theory, algebraic geometry, and mirror symmetry. Recently Gross, Hacking, Keel and Kontsevich released a preprint introducing mirror symmetry techniques into the subject which resolved several long-standing conjectures, including the construction of canonical bases for cluster algebras and positivity of the Laurent phenomenon. This preprint reformulates the basic construction of cluster algebras in terms of scattering diagrams (or wall-crossing structures). This leads to the proofs of the conjectures and to new constructions of elements of cluster algebras. But fundamentally they provide a new tool for thinking about cluster algebras.

The workshop will bring together many of the different users of cluster algebras to achieve a synthesis of these new techniques with many of the different aspects of the subject. There will be lecture series on the new techniques, and other lecture series on connections with Lie theory, quiver representation theory, mirror symmetry, string theory, and stability conditions.

In a recent paper, Marcus, Spielman and Srivastava solve the Kadison-Singer Problem by proving Weaver's KS2 conjecture and the Paving Conjecture. Their proof involved a technique they called the “method of interlacing families of polynomials” and a “barrier function” approach to proving bounds on the locations of the zeros of real stable polynomials. Using these techniques, they have also proved that there are infinite families of Ramanujan graphs of every degree, and they have developed a very simple proof of Bourgain and Tzafriri's Restricted Invertibility Theorem. The goal of this workshop is to help build upon this recent development by bringing together researchers from the disparate areas related to these techniques, including Functional Analysis, Spectral Graph Theory, Free Probability, Convex Optimization, Discrepancy Theory, and Real Algebraic Geometry.

Since their introduction just two years ago, perfectoid spaces have played a crucial role in a number of striking advances in arithmetic algebraic geometry: the proof of Deligne's weight-monodromy conjecture for complete intersections in toric varieties; the development of p-adic Hodge theory for rigid analytic spaces;  a p-adic analogue of Riemann's classification of abelian varieties over the complex numbers; and the construction of Galois representations for torsion classes in the cohomology of many locally symmetric spaces (for instance arithmetic hyperbolic 3-manifolds). We will start the week with an exposition of the foundations of the theory of perfectoid spaces, with the aim of teaching novices to work with them. Then we will discuss their current and potential applications.

Recently there has been substantial progress in our understanding of the related questions of which hyperbolic groups are cubulated on the one hand, and which contain a surface subgroup on the other. The most spectacular combination of these two ideas has been in 3-manifold topology, which has seen the resolution of many long-standing conjectures. In turn, the resolution of these conjectures has led to a new point of view in geometric group theory, and the introduction of powerful new tools and structures. The goal of this conference will be to explore the further potential of these new tools and perspectives, and to encourage communication between researchers working in various related fields.

The workshop will focus on recent developments concerning various quantitative aspects of "thin groups". These are discrete subgroups of semisimple Lie groups which are both « big » (i.e. Zariski dense) and « small » (i.e. of infinite co-volume). This dual nature leads to many intricate questions. Over the past few years, many new ideas and techniques, arising in particular from arithmetic combinatorics, have been involved in the study of such groups, leading for instance to far-reaching generalizations of the strong approximation theorem in which congruence quotients are shown to exhibit a spectral gap (super-strong approximation).

Simultaneously and sometimes surprisingly, the study of thin groups turns out to be of fundamental importance in a variety of subjects, including equidistribution of homogeneous flows and lattice points counting problems, dynamics on Teichmuller space, the Bourgain-Gamburd-Sarnak sieve in orbit, and arithmetic or geometric properties of certain types of monodromy groups and coverings. The workshop will gather a variety of experts from group theory, number theory, ergodic theory and harmonic analysis to present the accomplishments to date to a broad audience and discuss directions for further study.

This workshop will focus on the ideas surrounding the recent solution to the Arf-Kervaire invariant problem in stable homotopy theory by Mike Hill, Mike Hopkins and Doug Ravenel. There will be talks on relevant aspects of equivariant stable homotopy theory, including the norm functor and the slice tower. The pertinent parts of chromatic homotopy theory will be covered including formal groups and formal $A$-modules, the Hopkins-Miller theorem, finite subgroups of Morava stabilizer groups and Ravenel's 1978 solution to the analogous problem at primes bigger than 3. There will also be several talks by the organizers giving a detailed account of the proof of the main theorem. Finally there will be a discussion of the questions raised by the unexpected statement of the theorem.




 

The mathematical study of the dynamics of the Einstein equations forms a central part of both partial differential equations and geometry, and is intimately related to our current physical understanding of gravitational collapse.

This workshop will concentrate on recently discovered relationships between Seiberg-Witten theory and contact geometry on 3 dimensional manifolds. One consequence of these relationships is a proof of the Weinstein conjecture in dimension 3. Another is an isomorphism between the Seiberg-Witten Floer (co)homology and embedded contact homology, the latter a form of Floer homology that was defined by Michael Hutchings. The over arching plan is to introduce the salient features of both the contact geometry side of the story and the Seiberg-Witten side, and then discuss how they are related.

This workshop is jointly funded by MSRI and the Clay Mathematics Institute.