-
Séminaire de Mathématiques Supérieures 2026: Universal Statistics in Number Theory (Montréal, Canada)
Organizers: Louis-Pierre Arguin (University of Oxford), Andrew Granville (Université de Montréal), Dimitris Koukoulopoulos (Université de Montréal), Matilde Lalin (Université de Montréal), Carlo Pagano (Concordia University), Elliott Paquette (McGill University), Frank Thorne (University of South Carolina)
One of the hottest topics in analytic number theory involves the use of statistics and probability in understanding different aspects of algebraic and analytic number theory, through various new lenses. This is reflected in some of the most exciting number theory research of the last few years (for example, of Bhargava, of Ellenberg and Venkatesh, of Alexander Smith, of Sawin and Wood, of Adam Harper, of Koukoulopoulos and Maynard, of Helfgott and Radziwill, of Pilatte,....). As a consequence the CRM will host a thematic semester Mar 2-July 3, 2026 on these topics involving some of the world leaders in the subject. Since this new area can roughly be split in two into Algebraic and Analytic, we will focus for two months on each, with the SMS school placed in the middle. The 2026 SMS will introduce junior mathematicians to important trends in number theory.
Updated on Oct 17, 2025 04:27 PM PDT -
Percolation and Lattice Models of Statistical Physics (Columbia University)
Organizers: Roland Bauerschmidt (New York University, Courant Institute), Tom Hutchcroft (California Institute of Technology) <p>The five largest clusters in critical site percolation on a large three-dimensional box</p>
<p>The five largest clusters in critical site percolation on a large three-dimensional box</p>Percolation and spin models such as the Ising model have a history that goes back over 100 years. The subject has taken a central role in probability theory over the last few decades, in particular through interactions with various other areas of mathematics. These include graph theory, theoretical
computer science, statistical physics, quantum field theory, complex analysis, partial differential equations, and geometric group theory. Through examples, the summer school aims to illustrate some of the successful techniques and ideas in the subject area.Updated on Aug 26, 2025 12:45 PM PDT -
Geometric Measure Theory (SLMath)
Organizers: Camillo De Lellis (Institute for Advanced Study), Guido De Philippis (Hausdorff Research Institute for Mathematics, University of Bonn)
The school will consist of three interrelated courses, aimed to introduce the main concepts in Geometric Measure Theory.
(1) Sets and measure in the Euclidean space, Guido De Philippis (Courant Institute of Mathematical Sciences)
(2) Theory of currents, Annalisa Massaccesi (University of Padua)
(3) Allard regularity theory, Camillo De Lellis (Institute of Advanced Study)Updated on Sep 25, 2025 02:36 PM PDT -
ICTP-INdAM-SLMath School: Mathematics For Machine Learning (Trieste, Italy)
Organizers: Claudio Arezzo (Abdus Salam International Centre for Theoretical Physics), Jean Barbier (Abdus Salam International Centre for Theoretical Physics), Filippo Bracci (Università di Roma Tor Vergata), LEAD Domenico Marinucci (Università di Roma Tor Vergata), Cristina Trombetti (CSEF and Università degli Studi di Napoli Federico II)
The aim of this summer school is to provide an introduction to theoretical ideas that have been developed with the objective of understanding machine learning methods and their domain of applicability. The focus will be on proof technique and general mathematical tools. The lecturers are two worldwide experts in the area and the material is regularly taught in Mathematics and Statistics Departments of the top world Universities.
Updated on Jul 23, 2025 02:08 PM PDT -
Random Growth Models, Phase Separation and Hamilton-Jacobi PDE (UC Berkeley)
Organizers: Alan Hammond (University of California, Berkeley), Fraydoun Rezakhanlou (University of California, Berkeley)Models of random growth and of the separation of phases occurring when one substance is suspended in another often evince universal features, in which scaling exponents are shared among a broad class of such models. A foothold for understanding such features is often offered by studying a few special models that are exactly solvable, which means that exact formulas of algebraic or integrable origin are available. Showing that a broader range of models also have the features is a task that may rely on a range of robust probabilistic or geometric tools. The summer school will offer an introduction to random growth and phase separation, with an emphasis on tools that offer the prospect of proving universality for a wider class of models.
Updated on Aug 26, 2025 02:14 PM PDT -
SLMath-Oxford-OIST School: Analysis of Partial Differential Equations (Okinawa, Japan)
Organizers: Ugur Abdulla (Okinawa Institute of Science and Technology), Gui-Qiang Chen (University of Oxford)
This two week summer school, jointly organized by SLMath with OIST, will offer the following two mini-courses:
- Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
This course will present some recent developments in the theory of divergence-measure fields via measure-theoretic analysis and its applications to the analysis of nonlinear PDEs of conservative form – nonlinear conservation laws. - Perron’s method and Wiener-type criteria in the potential theory of elliptic and parabolic PDEs
This course will present some recent developments precisely characterizing the regularity of the point at ∞ for second order elliptic and parabolic PDEs and broadly extending the role of the Wiener test in classical analysis.
Updated on Dec 03, 2025 10:44 AM PST - Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
-
John Tukey Summer Graduate School: Mathematics of Generative Models (SLMath)
Organizers: Jianfeng Lu (Duke University), Eric Vanden-Eijnden (New York University, Courant Institute) <p>Artificial image generation by flow-based generative models starting from noise</p>
<p>Artificial image generation by flow-based generative models starting from noise</p>The overarching goal of this summer school is to expose students to the latest developments in the mathematics of generative models. Our ultimate goal is to teach them how to conduct research in this exciting area in machine learning and use their knowledge to make contributions to applied mathematics using these new tools.
Updated on Nov 06, 2025 09:24 AM PST -
Dynamical Systems for Machine Learning and AI (IBM Yorktown)
Organizers: Haoyang Cao (Johns Hopkins University), Soumyadip Ghosh (IBM Thomas J. Watson Research Center), LEAD Yingdong Lu (IBM Thomas J. Watson Research Center), Tomasz Nowicki (IBM Thomas J. Watson Research Center), Yunan Yang (Cornell University)
This Summer Graduate School aims to introducing graduate students to some aspects of contemporary modeling and analysis of dynamical systems in their interactions with machine learning and artificial intelligence (AI) applications.
Updated on Aug 21, 2025 12:08 PM PDT -
Singularities in Commutative Algebra Through Cohomological Methods (SLMath)
Organizers: Benjamin Briggs (Imperial College, London), Eloísa Grifo (University of Nebraska), Josh Pollitz (Syracuse University) <p>Homotopy measures how spheres can be tangled in spaces; the logo shows a sphere tangled in a grove of California redwoods<br />The background painting is “Giant Redwood Trees of California” by Albert Bierstadt in 1874</p>
<p>Homotopy measures how spheres can be tangled in spaces; the logo shows a sphere tangled in a grove of California redwoods<br />The background painting is “Giant Redwood Trees of California” by Albert Bierstadt in 1874</p>The goal of this school will be to introduce students to several powerful cohomological tools that were brought to commutative algebra by Avramov in the 80s and 90s: Lie algebra methods from homotopy theory, and support theoretic methods from the representation theory of finite groups. These tools have have seen a huge array of applications that continue to grow, with several major developments in recent years, opening new connections to algebraic topology, noncommutative algebraic geometry, and representation theory.
Updated on Oct 03, 2025 10:23 AM PDT -
Moduli of Varieties (SLMath)
Organizers: Kenneth Ascher (University of California, Irvine), Dori Bejleri (University of Maryland), Kristin DeVleming (University of California, San Diego)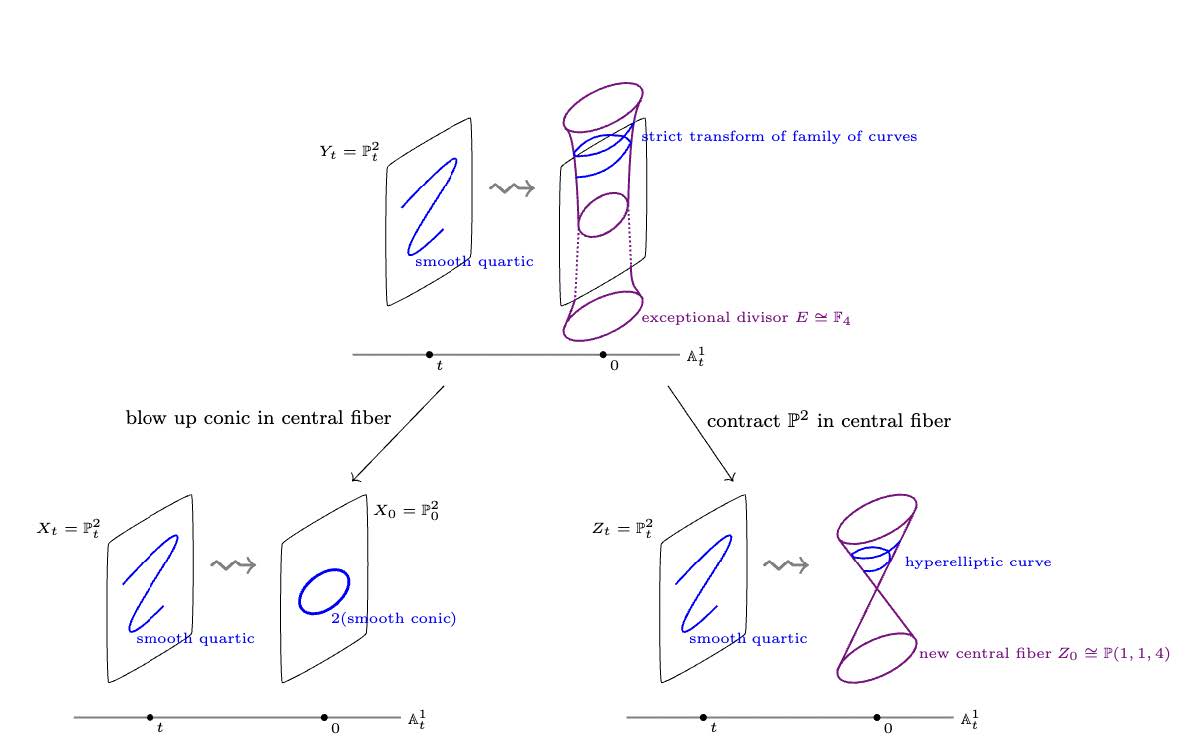 <p>A wall-crossing in a moduli problem</p>
<p>A wall-crossing in a moduli problem</p>One of the central problems in algebraic geometry is to classify so-called algebraic varieties: geometric shapes cut out by polynomial equations. Algebraic varieties are parametrized by certain moduli spaces (roughly: parameter spaces whose points correspond to these different varieties). The geometry of these moduli spaces encodes the ways of continuously deforming these shapes. Furthermore, classification questions for algebraic varieties often boil down to understanding the geometry of these moduli spaces. In the past few years, powerful new tools have been developed in moduli theory, especially for higher dimensional varieties – those which are of complex dimension at least two. The goal of this summer school is to provide an introduction to many of these recently emerging breakthroughs to enable graduate students to begin working in this area. The program will be motivated and often guided by examples and is intended to be accessible to a wide variety of students
Updated on Oct 07, 2025 09:46 AM PDT
|
|
Upcoming Summer Graduate Schools |
