-
Workshop Critical Issues in Mathematics Education 2026: Math Literacy for 21st Century Citizenship - Part II
Organizers: Robert Berry (Indiana University), Josue Cordones (Bronx Collaborative High School), Megan Franke (University of California, Los Angeles), Maisie Gholson (University of Michigan), Courtney Ginsberg (Math for America), Mark Hoover (University of Michigan), Yvonne Lai (University of Nebraska), LEAD Maisha Moses (The Young People's Project), LEAD Benjamin Moynihan (The Algebra Project, Inc.), Aris Winger (Georgia Gwinnett College)Building on the vision Bob Moses set out in the 1993 Algebra Initiative Colloquium, the 2025 Critical Issues in Mathematics Education (CIME) Workshop celebrated the legacy of Moses’ call for a mathematics literacy that supports citizenship in the 21st century. A mathematics towards citizenship has proved elusive as a goal for mathematicians, mathematics educators, researchers, students, teachers, and leaders—even as efforts among different individuals, organizations, and communities labor for greater access to high-quality mathematics learning experiences. The 2026 CIME Workshop, Math Literacy for 21st Century Citizenship - Part II, endeavors to design opportunities for learning, collaborating, and struggling towards a mathematics for lived citizenship, as a theme and organizing principle for communities across the Nation.
For Moses, the notion of lived citizenship is not simply a matter of gaining legal status but of demanding that the legal status be meaningful. Thus mathematics literacy for lived or participatory citizenship might be thought of to include contributing to your community, not just being part of a community, and beyond belonging, to actively participate in making your community better, in making life better for others.
The conception of mathematics for lived citizenship is an important foundation for the goals for the 2026 CIME Workshop, in order to envision the development of coordinated actions in the short and long term within the mathematics and mathematics education communities. To ground and catalyze these efforts, we invite participants to consider a mathematics for lived citizenship through three foundational ideas:
- Claiming mathematics -- establishing agency in and ownership of math.
- Building Agency -- claiming and leveraging mathematics knowledge to overcome present day, generational, community, and national challenges.
- Collaboration and collective effort -- using mathematics literacy to make systemic change.
Three questions will guide our work:
- How does the unfolding history of mathematics impact lived citizenship?
- How do we understand the relationship between mathematical flourishing and the evolution of vibrant democracy in the United States?
- In light of the above two questions, how do we reimagine our roles, responsibilities, and actions in the short and long term?
Updated on Jan 07, 2026 11:06 AM PST -
Summer Graduate School Séminaire de Mathématiques Supérieures 2026: Universal Statistics in Number Theory (Montréal, Canada)
Organizers: Louis-Pierre Arguin (University of Oxford), Andrew Granville (Université de Montréal), Dimitris Koukoulopoulos (Université de Montréal), Matilde Lalin (Université de Montréal), Carlo Pagano (Concordia University), Elliott Paquette (McGill University), Frank Thorne (University of South Carolina)
One of the hottest topics in analytic number theory involves the use of statistics and probability in understanding different aspects of algebraic and analytic number theory, through various new lenses. This is reflected in some of the most exciting number theory research of the last few years (for example, of Bhargava, of Ellenberg and Venkatesh, of Alexander Smith, of Sawin and Wood, of Adam Harper, of Koukoulopoulos and Maynard, of Helfgott and Radziwill, of Pilatte,....). As a consequence the CRM will host a thematic semester Mar 2-July 3, 2026 on these topics involving some of the world leaders in the subject. Since this new area can roughly be split in two into Algebraic and Analytic, we will focus for two months on each, with the SMS school placed in the middle. The 2026 SMS will introduce junior mathematicians to important trends in number theory.
Updated on Oct 17, 2025 04:27 PM PDT -
Summer Graduate School Percolation and Lattice Models of Statistical Physics (Columbia University)
Organizers: Roland Bauerschmidt (New York University, Courant Institute), Tom Hutchcroft (California Institute of Technology) <p>The five largest clusters in critical site percolation on a large three-dimensional box</p>
<p>The five largest clusters in critical site percolation on a large three-dimensional box</p>Percolation and spin models such as the Ising model have a history that goes back over 100 years. The subject has taken a central role in probability theory over the last few decades, in particular through interactions with various other areas of mathematics. These include graph theory, theoretical
computer science, statistical physics, quantum field theory, complex analysis, partial differential equations, and geometric group theory. Through examples, the summer school aims to illustrate some of the successful techniques and ideas in the subject area.Updated on Aug 26, 2025 12:45 PM PDT -
MSRI-UP MSRI-UP 2026: Numerical Methods for Differential Equations
Organizers: LEAD Alexander Diaz-Lopez (Villanova University), Maria Mercedes Franco (Queensborough Community College (CUNY)), Rebecca Garcia (Colorado College), Johnny Guzman (Brown University), Candice Price (Smith College), Robin Wilson (Loyola Marymount University)The MSRI-UP summer program is designed to serve a diverse group of undergraduate students who would like to conduct research in the mathematical sciences.
In 2026, MSRI-UP will focus on Numerical Methods for Differential Equations The research program will be led by Dr. Johnny Guzman of Brown University.
Updated on Dec 17, 2025 04:12 PM PST -
Summer Graduate School Random Growth Models, Phase Separation and Hamilton-Jacobi PDE (UC Berkeley)
Organizers: Alan Hammond (University of California, Berkeley), Fraydoun Rezakhanlou (University of California, Berkeley)Models of random growth and of the separation of phases occurring when one substance is suspended in another often evince universal features, in which scaling exponents are shared among a broad class of such models. A foothold for understanding such features is often offered by studying a few special models that are exactly solvable, which means that exact formulas of algebraic or integrable origin are available. Showing that a broader range of models also have the features is a task that may rely on a range of robust probabilistic or geometric tools. The summer school will offer an introduction to random growth and phase separation, with an emphasis on tools that offer the prospect of proving universality for a wider class of models.
Updated on Aug 26, 2025 02:14 PM PDT -
Summer Graduate School ICTP-INdAM-SLMath School: Mathematics For Machine Learning (Trieste, Italy)
Organizers: Claudio Arezzo (Abdus Salam International Centre for Theoretical Physics), Jean Barbier (Abdus Salam International Centre for Theoretical Physics), Filippo Bracci (Università di Roma Tor Vergata), LEAD Domenico Marinucci (Università di Roma Tor Vergata), Cristina Trombetti (CSEF and Università degli Studi di Napoli Federico II)
The aim of this summer school is to provide an introduction to theoretical ideas that have been developed with the objective of understanding machine learning methods and their domain of applicability. The focus will be on proof technique and general mathematical tools. The lecturers are two worldwide experts in the area and the material is regularly taught in Mathematics and Statistics Departments of the top world Universities.
Updated on Jan 05, 2026 03:53 PM PST -
Summer Graduate School John Tukey Summer Graduate School: Mathematics of Generative Models (SLMath)
Organizers: Jianfeng Lu (Duke University), Eric Vanden-Eijnden (New York University, Courant Institute) <p>Artificial image generation by flow-based generative models starting from noise</p>
<p>Artificial image generation by flow-based generative models starting from noise</p>The overarching goal of this summer school is to expose students to the latest developments in the mathematics of generative models. Our ultimate goal is to teach them how to conduct research in this exciting area in machine learning and use their knowledge to make contributions to applied mathematics using these new tools.
Updated on Nov 06, 2025 09:24 AM PST -
Summer Graduate School SLMath-Oxford-OIST School: Analysis of Partial Differential Equations (Okinawa, Japan)
Organizers: Ugur Abdulla (Okinawa Institute of Science and Technology), Gui-Qiang Chen (University of Oxford)
This two week summer school, jointly organized by SLMath with OIST, will offer the following two mini-courses:
- Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
This course will present some recent developments in the theory of divergence-measure fields via measure-theoretic analysis and its applications to the analysis of nonlinear PDEs of conservative form – nonlinear conservation laws. - Perron’s method and Wiener-type criteria in the potential theory of elliptic and parabolic PDEs
This course will present some recent developments precisely characterizing the regularity of the point at ∞ for second order elliptic and parabolic PDEs and broadly extending the role of the Wiener test in classical analysis.
Updated on Dec 03, 2025 10:44 AM PST - Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
-
Summer Graduate School Singularities in Commutative Algebra Through Cohomological Methods (SLMath)
Organizers: Benjamin Briggs (Imperial College, London), Eloísa Grifo (University of Nebraska), Josh Pollitz (Syracuse University) <p>Homotopy measures how spheres can be tangled in spaces; the logo shows a sphere tangled in a grove of California redwoods<br />The background painting is “Giant Redwood Trees of California” by Albert Bierstadt in 1874</p>
<p>Homotopy measures how spheres can be tangled in spaces; the logo shows a sphere tangled in a grove of California redwoods<br />The background painting is “Giant Redwood Trees of California” by Albert Bierstadt in 1874</p>The goal of this school will be to introduce students to several powerful cohomological tools that were brought to commutative algebra by Avramov in the 80s and 90s: Lie algebra methods from homotopy theory, and support theoretic methods from the representation theory of finite groups. These tools have have seen a huge array of applications that continue to grow, with several major developments in recent years, opening new connections to algebraic topology, noncommutative algebraic geometry, and representation theory.
Updated on Oct 03, 2025 10:23 AM PDT -
Summer Graduate School Dynamical Systems for Machine Learning and AI (IBM Yorktown)
Organizers: Haoyang Cao (Johns Hopkins University), Soumyadip Ghosh (IBM Thomas J. Watson Research Center), LEAD Yingdong Lu (IBM Thomas J. Watson Research Center), Tomasz Nowicki (IBM Thomas J. Watson Research Center), Yunan Yang (Cornell University)
This Summer Graduate School aims to introducing graduate students to some aspects of contemporary modeling and analysis of dynamical systems in their interactions with machine learning and artificial intelligence (AI) applications.
Updated on Aug 21, 2025 12:08 PM PDT -
Summer Graduate School Moduli of Varieties (SLMath)
Organizers: Kenneth Ascher (University of California, Irvine), Dori Bejleri (University of Maryland), Kristin DeVleming (University of California, San Diego)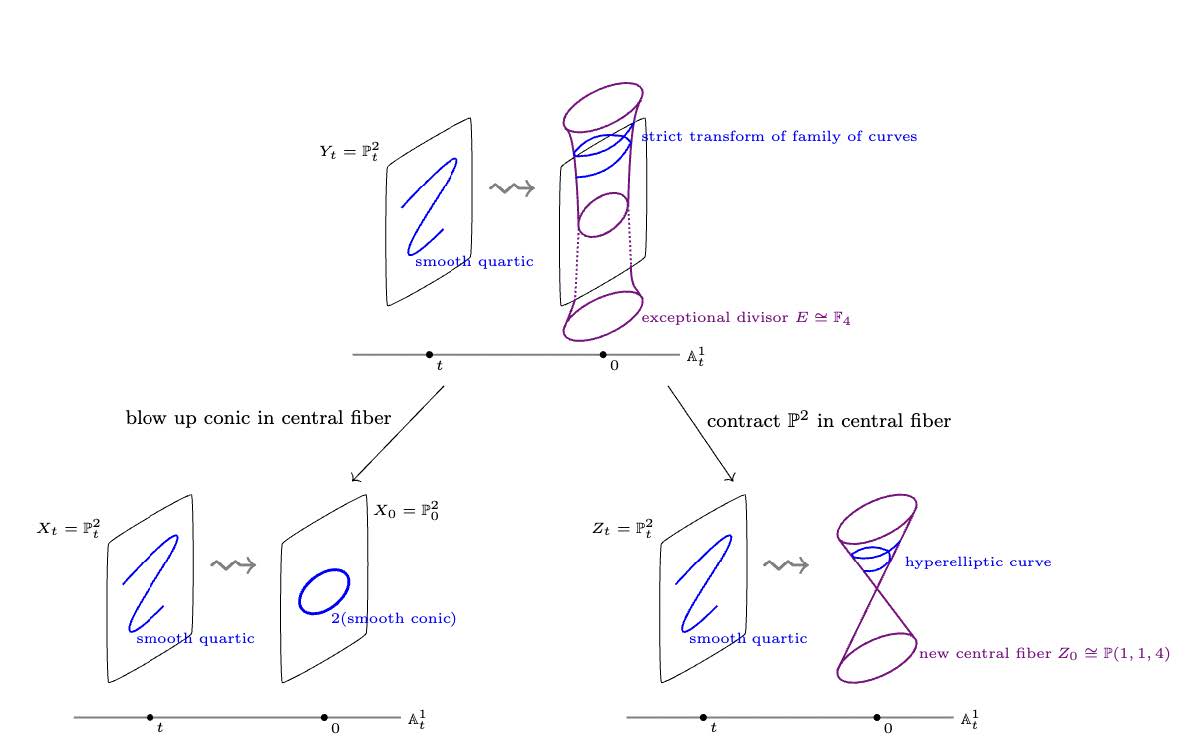 <p>A wall-crossing in a moduli problem</p>
<p>A wall-crossing in a moduli problem</p>One of the central problems in algebraic geometry is to classify so-called algebraic varieties: geometric shapes cut out by polynomial equations. Algebraic varieties are parametrized by certain moduli spaces (roughly: parameter spaces whose points correspond to these different varieties). The geometry of these moduli spaces encodes the ways of continuously deforming these shapes. Furthermore, classification questions for algebraic varieties often boil down to understanding the geometry of these moduli spaces. In the past few years, powerful new tools have been developed in moduli theory, especially for higher dimensional varieties – those which are of complex dimension at least two. The goal of this summer school is to provide an introduction to many of these recently emerging breakthroughs to enable graduate students to begin working in this area. The program will be motivated and often guided by examples and is intended to be accessible to a wide variety of students
Updated on Oct 07, 2025 09:46 AM PDT
Past Educational Events
-
Summer Graduate School Topological and Geometric Structures in Low Dimensions (SLMath)
Organizers: LEAD Kenneth Bromberg (University of Utah), Kathryn Mann (Cornell University) <p>Laminations arise naturally in hyperbolic geometry and (pseudo-) Anosov flows [Image by Jeffrey Brock]</p>
<p>Laminations arise naturally in hyperbolic geometry and (pseudo-) Anosov flows [Image by Jeffrey Brock]</p>This school will serve as an introduction to the SLMath semester “Topological and Geometric Structures in Low-Dimensions”. The school consists of two mini-courses: one on Teichmüller Theory and Hyperbolic 3-Manifolds and the other on Anosov Flows on Geometric 3-Manifolds. Both topics lie at the interface of low-dimensional geometric topology (specifically, surfaces, foliations, and 3-manifolds) and low-dimensional dynamics. The first course will be targeted towards students who have completed the standard first year graduate courses in geometry, topology, and analysis while the second course will geared towards more advanced students who are closer to beginning research. However, we expect that all students will benefit from both courses.
Updated on Nov 03, 2025 12:23 PM PST -
Summer Graduate School Geometry and Dynamics in Higher Rank Lie Groups (UC Berkeley)
Organizers: Richard Canary (University of Michigan), Sara Maloni (University of Virginia), Wenyu Pan (University of Toronto; University of Toronto), Cagri Sert (University of Zurich), LEAD Tengren Zhang (National University of Singapore)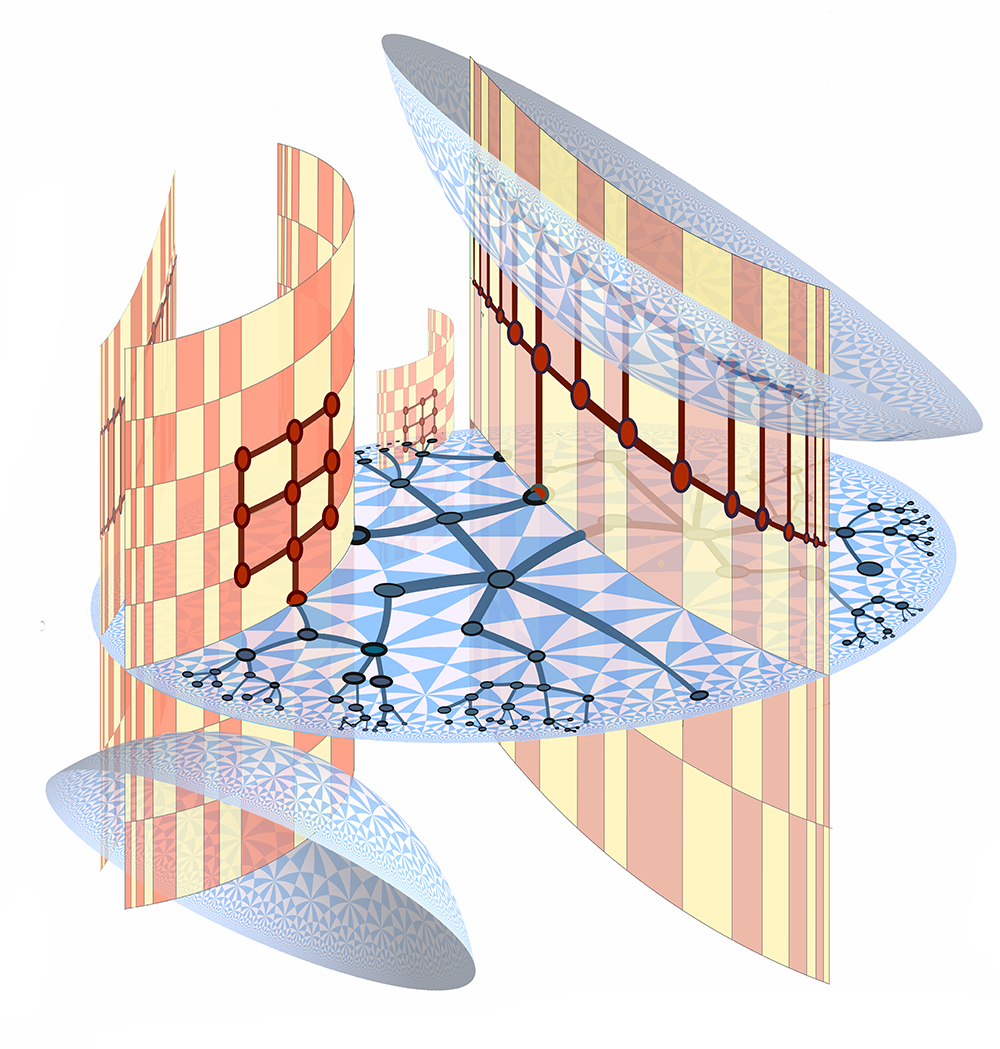 <p>Flats and hyperbolic planes in a higher rank symmetric space</p> Drawn by Steve Trettel.
<p>Flats and hyperbolic planes in a higher rank symmetric space</p> Drawn by Steve Trettel.Lie groups are central objects in modern mathematics; they arise as the automorphism groups of many homogeneous spaces, such as flag manifolds and Riemannian symmetric spaces. Often, one can construct manifolds locally modelled on these homogeneous spaces by taking quotients of their subsets by discrete subgroups of their automorphism groups. Studying such discrete subgroups of Lie groups is an active and growing area of mathematical research. The objective of this summer school is to introduce young researchers to a class of discrete subgroups of Lie groups, called Anosov subgroups.
Updated on Nov 03, 2025 01:16 PM PST -
Summer Graduate School Computer Assisted Proofs in Applied Mathematics (SLMath)
Organizers: LEAD Jonathan Jaquette (New Jersey Institute of Technology), Evelyn Sander (George Mason University)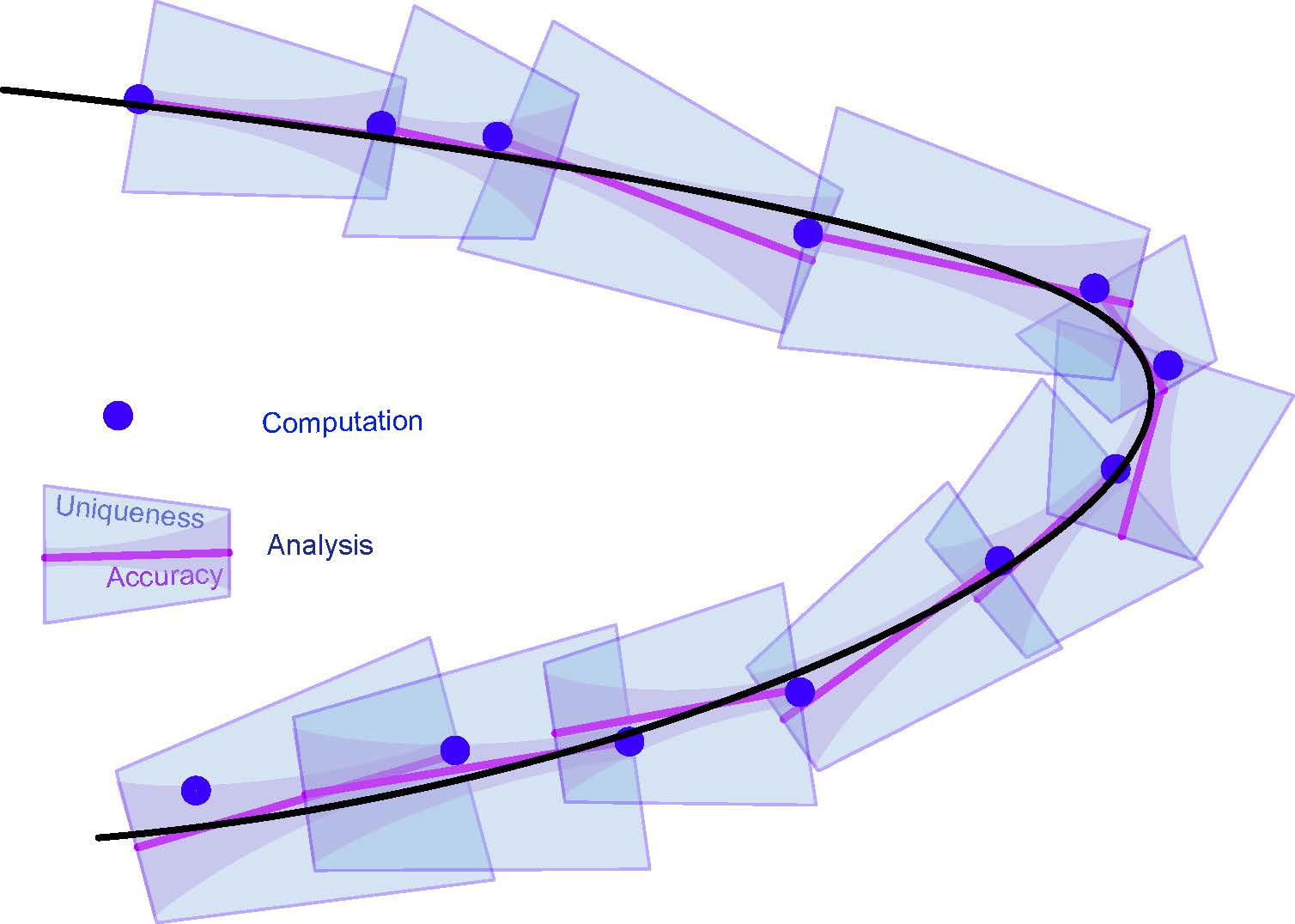
One of the core elements of applied mathematics is mathematical modeling consisting of nonlinear equations such as ODEs, and PDEs. A fundamental difficulty which arises is that most nonlinear models cannot be solved in closed form. Computer assisted proofs are at the forefront of modern mathematics and have led to many important recent mathematical advances. They provide a way of melding analytical techniques with numerical methods, in order to provide rigorous statements for mathematical models that could not be treated by either method alone. In this summer school, students will review standard computational and analytical techniques, learn to combine these techniques with more specialized methods of interval arithmetic, and apply these methods to establish rigorous results in otherwise intractable problems
Updated on Nov 03, 2025 01:45 PM PST -
Summer Graduate School Noncommutative Algebraic Geometry (Antwerp, Belgium)
Organizers: Pieter Belmans (University of Luxembourg), Lander Hermans (Universiteit Antwerp), Wendy Lowen (Universiteit Antwerpen), Arne Mertens (Universiteit Antwerp), Michel VAN DEN BERGH (Hasselt University), Špela Špenko (Université Libre de Bruxelles)
The school will consist of two courses: Homological Mirror Symmetry and Algebraic Models for Spaces. These courses will be planned and taught by organisers with the help of teaching assistants for the problem sessions. The school will be aimed at a wide range of graduate students, from students with a Bachelor degree to beginning PhD students. The lectures and problem sessions will be complemented by a poster session in week one and a total of four introductory research talks on Friday afternoons.
Updated on May 22, 2025 10:57 AM PDT -
Summer Graduate School Graphical Models in Algebraic Combinatorics (SLMath)
Organizers: Christian Gaetz (University of California, Berkeley), David Keating (University of Illinois at Urbana-Champaign), Melissa Sherman-Bennett (University of California, Davis), LEAD Anna Weigandt (University of Minnesota)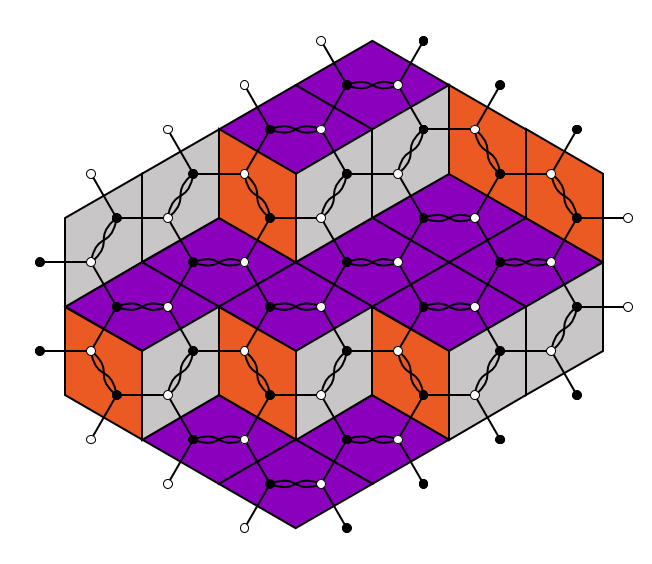 <p>A plane partition and an hourglass plabic graph</p>
<p>A plane partition and an hourglass plabic graph</p>This school will introduce students to a range of powerful combinatorial tools used to understand algebraic objects ranging from the homogeneous coordinate ring of the Grassmannian to symmetric functions. The summer school will center around two main lecture series "Webs and Plabic Graphs" and "Vertex Models and Applications". While the exact applications differ, both courses will center on graphical models for algebraic problems closely related to Grassmannian and its generalizations. This school will be accessible to a wide range of students. Students will leave the school with a solid grasp of the combinatorics of webs, plabic graphs, and the six-vertex model, an understanding of their algebraic applications, and a taste of current research directions.
Updated on Jul 02, 2025 10:42 AM PDT -
Summer Graduate School New Perspectives on Discriminants and Applications (Leipzig, Germany)
Organizers: Eliana Duarte (Centro de Matemática da Universidade do Porto), Serkan Hosten (San Francisco State University), Simon Telen (Max-Planck-Institut)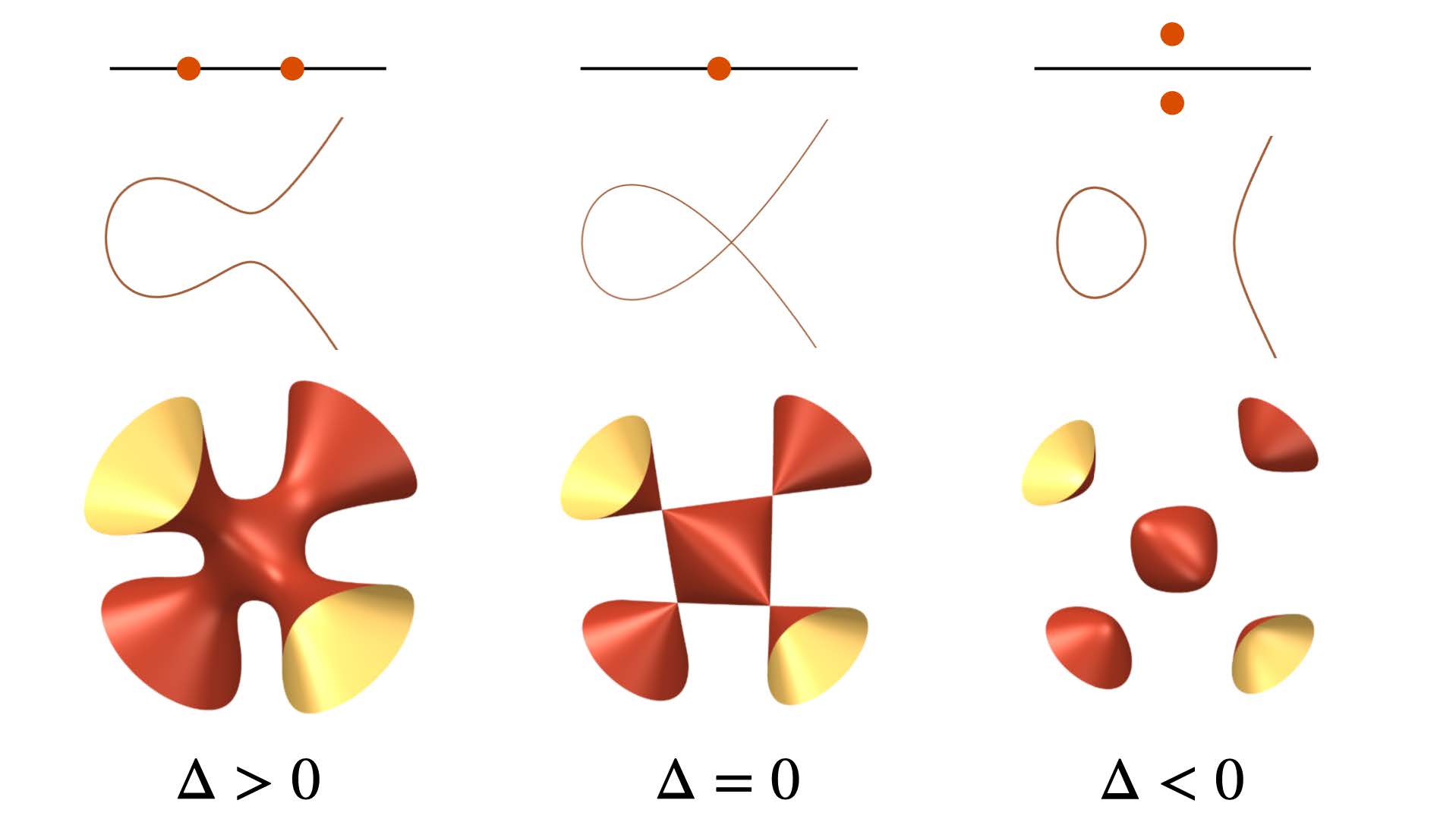 <p>The discriminant ∆ detects singular varieties. The picture shows three different scenarios: solutions of quadratic polynomials, cubic plane curves and cubic surfaces.</p>
<p>The discriminant ∆ detects singular varieties. The picture shows three different scenarios: solutions of quadratic polynomials, cubic plane curves and cubic surfaces.</p>This summer school will offer a hands-on introduction to discriminants, with a view towards modern applications. Starting from the basics of computational algebraic geometry and toric geometry, the school will gently introduce participants to the foundations of discriminants. A particular emphasis will be put on computing discriminants of polynomial systems using computer algebra software. Then, we will dive into three applications of discriminants: algebraic statistics, geometric modeling, and particle physics. Here, discriminants contribute to the study of maximum likelihood estimation, to finding practical parametrizations of geometric objects, and to computations of scattering amplitudes. We will explain recently discovered unexpected connections between these three applications. In addition to lectures, the summer school will have daily collaborative exercise sessions which will be guided by the teaching assistants and will include software demonstrations.
Updated on Jul 03, 2025 09:26 AM PDT -
Summer Graduate School Mathematics of Sea Ice and Polar Ecosystems (Fairbanks, Alaska)
Organizers: Kenneth Golden (University of Utah), Jody Reimer (University of Utah) From micro to macro, sea ice supports life in the polar regions. Left: illustration of the porous sea ice microstructure, home to a microbial community of ice endemic organisms including bacteria and algae. Right: two penguins on Antarctic sea ice.
From micro to macro, sea ice supports life in the polar regions. Left: illustration of the porous sea ice microstructure, home to a microbial community of ice endemic organisms including bacteria and algae. Right: two penguins on Antarctic sea ice.In this summer school, students will be introduced to mathematical and computational modeling of sea ice and polar ecosystems. As a material, sea ice is a multiscale composite structured on length scales ranging from tenths of millimeters to tens of kilometers. From tiny brine inclusions and surface melt ponds of increasing complexity, to ice floes of varying sizes in a seawater host, a principal challenge is how to find sea ice effective properties that are relevant to larger scale models, given data on smaller scale structures. Similarly, the sea ice ecosystem ranges from algae living in the brine inclusions to charismatic megafauna like penguins and polar bears, whose diets depend critically, down the line, on the tiny sea ice extremophiles. The dynamics of sea ice microbial communities are regulated by the physics of the ice microstructure, and, in turn, many of these microbes modify their environment by secreting extracellular polymeric substances. In addition to sea ice and its ecosystems, we will consider broader mathematical models including energy balance models, tipping points, and global circulation models.
Updated on Jun 10, 2025 09:42 AM PDT -
MSRI-UP MSRI-UP 2025: Quantitative Justice
Organizers: Alexander Diaz-Lopez (Villanova University), Maria Mercedes Franco (Queensborough Community College (CUNY)), Rebecca Garcia (Colorado College), Omayra Ortega (Sonoma State University), Candice Price (Smith College), LEAD Robin Wilson (Loyola Marymount University)The MSRI-UP summer program is designed to serve a diverse group of undergraduate students who would like to conduct research in the mathematical sciences.
In 2025, MSRI-UP will focus on Quantitative Justice. The research program will be led by Dr. Omayra Y. Ortega, Associate Professor in the Department of Mathematics at Sonoma State University.
Updated on Dec 11, 2025 12:32 PM PST -
Summer Graduate School Statistical Optimal Transport (SLMath)
Organizers: LEAD Promit Ghosal (University of Chicago), Jonathan Niles Weed (New York University, Courant Institute), Marcel Nutz (Columbia University)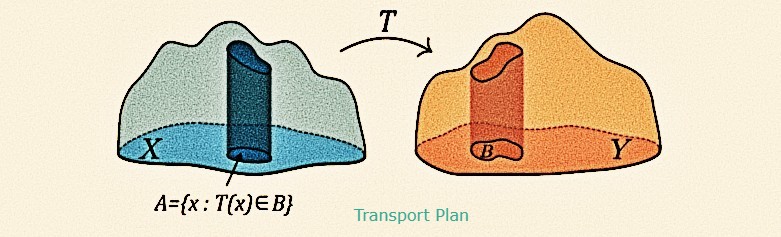
This summer school offers an exceptional opportunity for participants to delve into the intricate realm of statistical optimal transport theory. This captivating field stands at the crossroads of multiple disciplines, drawing from a rich tapestry of mathematical insights from diverse subjects, including partial differential equations, stochastic analysis, convex geometry, statistics, and machine learning, crafting a vibrant and interdisciplinary landscape. The foremost objective of this summer school is to create a dynamic learning environment that unites students from diverse backgrounds such as PDE theory, probability, or optimal transport.
Updated on Nov 03, 2025 01:32 PM PST -
Summer Graduate School Local Limits of Random Graphs (Paris-Saclay University, France)
Organizers: Ainhoa Aparicio-Monforte (Fondation Mathématique Jacques Hadamard (FMJH)), Alexandra Genesco (Fondation Mathématique Jacques Hadamard (FMJH)), LEAD Pascal Massart (Fondation Mathématique Jacques Hadamard (FMJH)) <p>A display of the evolution of an Erdos-Renyi random graph . </p>
<p>A display of the evolution of an Erdos-Renyi random graph . </p>Random graphs are ubiquitous in modern probability theory. Besides their intrinsic mathematical beauty, they are also used to model complex networks. In the early 2000’s, I. Benjamini and O. Schramm introduced a mathematical framework in which they endowed the set of locally finite rooted connected graphs with the structure of a Polish space, called the local topology. The goal of this summer school is to introduce the framework of local limits of random graphs, the concepts of Benjamini-Schramm (or unbiased) limits and unimodularity, as well as the most important applications. The lectures will be delivered by Nicolas Curien (Prof. Paris-Saclay University) and Justin Salez (Prof. Université Paris-Dauphine) and will be complemented by many problem sessions, where students will work in small groups under the guidance of teaching assistants, who are researchers in the field.
Updated on Jun 06, 2025 09:24 AM PDT -
Summer Graduate School 2025 PIMS-CRM Summer School in Probability (Vancouver, Canada)
Organizers: Louigi Addario-Berry (McGill University), Omer Angel (University of British Columbia), Mathav Murugan (University of British Columbia), Gordon Slade (University of British Columbia)The Summer Schools in Probability are a highlight of Canadian probability and are internationally significant. Launched by PIMS in 2004, the school takes the form of two main 4-week courses along with three mini-courses. The schools have played a major role in the development of an exceptionally strong community of young probabilist in Canada, North America and overseas. This will be the 13th time this school has run.
Updated on Jul 01, 2025 11:35 AM PDT -
Summer Graduate School Séminaire de Mathématiques Supérieures 2025: An Introduction to Recent Trends in Commutative Algebra (Toronto, Canada)
Organizers: Sergio Da Silva (Virginia State University), Federico Galetto (Cleveland State University), Elena Guardo (Università di Catania), Megumi Harada (McMaster University), Patricia Klein (Texas A & M University), Jenna Rajchgot (McMaster University), Adam Van Tuyl (McMaster University)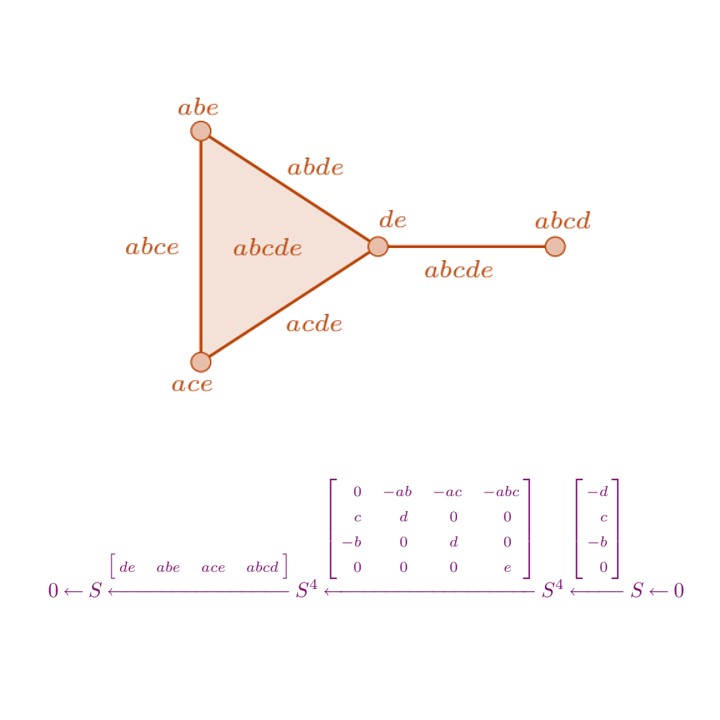 <p>A minimal free resolution supported on a simplicial complex</p>
<p>A minimal free resolution supported on a simplicial complex</p>The 2025 SMS will allow graduate students to learn about a number of recent trends and advances in the field of commutative algebra. The aim of the SMS is to provide an “on-ramp” for graduate students interested in algebra, combinatorics, and/or algebraic combinatorics to learn more about commutative algebra’s interaction with these fields. The introductory courses will introduce fundamental skills in commutative algebra, the more intermediate courses will expose students to cutting-edge research in the field. The school will focus on four topics within commutative algebra: Combinatorial Methods, Homological Methods, Computational Methods, and Characteristic p Methods. The SMS will provide both a series of introductory lectures and intermediate/advanced lectures from leaders in one of the four areas. The lectures will include a series of problem sessions that will allow participants to develop and hone their skills in these areas, which will be especially helpful for new people to the field. Participants will be encouraged to work collaboratively, both to enhance their own mathematical networks as well as to promote future collaborations beyond the school.
Updated on Feb 19, 2025 04:14 PM PST -
Workshop Critical Issues in Mathematics Education 2025: K-12 Mathematics Literacy for 21st-Century Citizenship
Organizers: David Barnes (National Council of Teachers of Mathematics (NCTM)), Marta Civil (University of Arizona), Josue Cordones (Bronx Collaborative High School), Bill Crombie (The Algebra Project), Courtney Ginsberg (Math for America), Mark Hoover (University of Michigan), Emille Lawrence (University of San Francisco), Maisha Moses (The Young People's Project), Benjamin Moynihan (The Algebra Project, Inc.), Karen Saxe (Macalester College), Robin Wilson (Loyola Marymount University), Aris Winger (Georgia Gwinnett College)Activist Bob Moses argued that mathematical literacy was the next civil rights front line. The 2025 CIME workshop will explore what mathematical literacy might mean and why it still matters for citizenship now and in the future. The workshop’s long-term impact relies on the participation of research mathematicians, mathematics educators, educational researchers, teachers of school mathematics, and policymakers working across different perspectives and roles to foster collaboration that will raise the floor for mathematical literacy for citizenship now and in the future.
Updated on Apr 10, 2025 09:12 AM PDT -
Workshop LatMath 2025 at IPAM
This research conference will feature plenary talks by leading researchers, career panels, professional development opportunities, and scientific sessions in the following areas: (1) Algebra/Number Theory, (2) Combinatorics, (3) Harmonic Analysis, PDEs & Differential Geometry, (4) Numerical Analysis and Computational Mathematics, (5) Machine Learning, (6) Mathematical Biology, (7) Statistics, Data Analysis, and (8) Math Education.
The goal of the conference is to encourage attendees to pursue careers in the mathematical sciences, to showcase research being conducted at the forefront of their fields, and, finally, to build a community around shared academic interests. The conference will be held on the UCLA campus in Los Angeles, CA.
LatMath is funded by the National Science Foundation Division of Mathematical Sciences, with additional support from generous sponsors.
Updated on Feb 26, 2025 10:50 AM PST -
Workshop Modern Math Workshop 2024
Updated on Jul 24, 2024 04:45 PM PDT -
Summer Graduate School Mathematical Spin Glass Theory (Courant, NY)
Organizers: Antonio Auffinger (Northwestern University), Wei-Kuo Chen (University of Minnesota), LEAD Eliran Subag (Weizmann Institute of Science)
While their original aim was to explain the strange behavior of certain magnetic alloys, the study of spin glass models has led to a far-reaching and beautiful physical theory whose techniques have been applied to a myriad of problems in theoretical computer science, statistics, optimization and biology. As many of the physical predictions can be formulated as purely mathematical questions, often extremely hard, about large random systems in high dimensions, in recent decades a new area of research has emerged in probability theory around these problems.
Mathematically, a mean-field spin glass model is a Gaussian process (random function) on the discrete hypercube or the sphere in high dimensions. A fundamental challenge in their analysis is, roughly speaking, to understand the size and structure of their super-level sets as the dimension tends to infinity, which are often studied through smooth objects like the free energy and Gibbs measure whose origin is in statistical physics. The aim of the summer school is to introduce students to landmark results on the latter while emphasizing the techniques and ideas that were developed to obtain them, as well as exposing the students to some recent research topics.
Updated on Apr 19, 2024 03:00 PM PDT -
Summer Graduate School Multigraded and differential graded methods in commutative algebra (St. Mary's College)
Organizers: Michael Brown (Auburn University), Claudia Miller (Syracuse University) Product of projective lines embedded in projective 3-space
Product of projective lines embedded in projective 3-spaceThis summer graduate school focuses on modern homological techniques in commutative algebra, specifically those involving multigraded and differential graded structures. These topics have a long and rich history, but neither is generally covered in graduate courses. Moreover, recent developments have exhibited exciting interplay between the two subjects.
The purpose of the school is to introduce the participants to modern themes on these topics, including Koszul duality for toric varieties and differential graded algebra structures on resolutions. The school will consist of two lectures each day and carefully planned problem sessions designed to reinforce the foundational material, with an emphasis on using computational tools such as the symbolic algebra program Macaulay2.
Updated on Aug 08, 2024 02:59 PM PDT -
Summer Graduate School Analysis of Partial Differential Equations (Okinawa Institute of Science and Technology)
Organizers: Ugur Abdulla (Okinawa Institute of Science and Technology), Gui-Qiang Chen (University of Oxford)This two week summer school, jointly organized by SLMath with OIST, will offer the following two mini-courses:
- Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
This course will present some recent developments in the theory of divergence-measure fields via measure-theoretic analysis and its applications to the analysis of nonlinear PDEs of conservative form – nonlinear conservation laws. - Perron’s method and Wiener-type criteria in the potential theory of elliptic and parabolic PDEs
This course will present some recent developments precisely characterizing the regularity of the point at ∞ for second order elliptic and parabolic PDEs and broadly extending the role of the Wiener test in classical analysis.
Updated on Sep 09, 2024 12:17 PM PDT - Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
-
Summer Graduate School Mathematics of General Relativity and Fluids (FORTH, Greece)
Organizers: LEAD Mihalis Dafermos (Princeton University), Grigorios Fournodavlos (University of Crete), Juhi Jang (University of Southern California), Igor Rodnianski (Princeton University)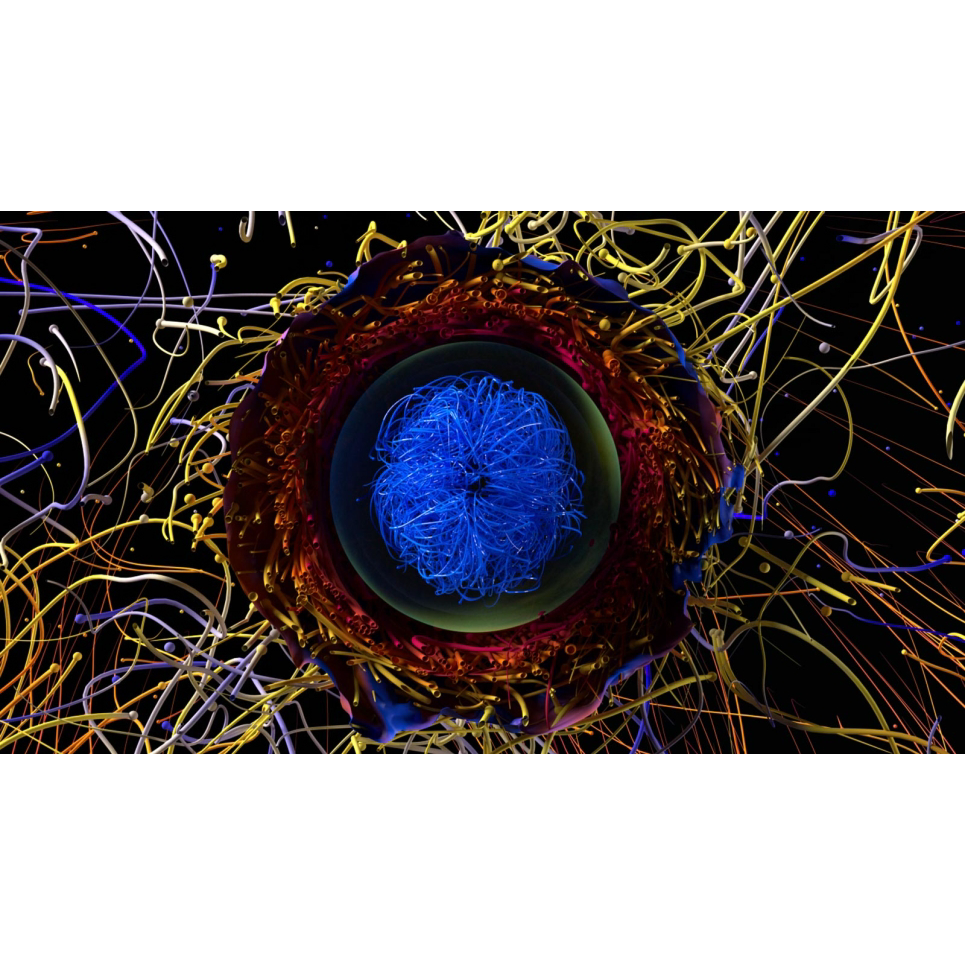 ALCF Visualization and Data Analytics Team; Adam Burrows and the Princeton Supernova Theory Group, Princeton University
ALCF Visualization and Data Analytics Team; Adam Burrows and the Princeton Supernova Theory Group, Princeton UniversityThis summer school will give an accessible introduction to the mathematical study of general relativity, a field which in the past has had barriers to entry due to its interdisciplinary nature, and whose study has been concentrated at specific institutions, to a wider audience of students studying at institutions throughout the U.S., Europe and Greece. Another goal of the summer school will be to demonstrate the common underlying mathematical themes in many problems which traditionally have been studied by separate research communities.
Updated on Oct 03, 2024 01:48 PM PDT -
Summer Graduate School Introduction to the Theory of Algebraic Curves (UC Berkeley)
Organizers: Izzet Coskun (University of Illinois, Chicago), Eric Larson (Brown University), LEAD Hannah Larson (University of California, Berkeley), Isabel Vogt (Brown University)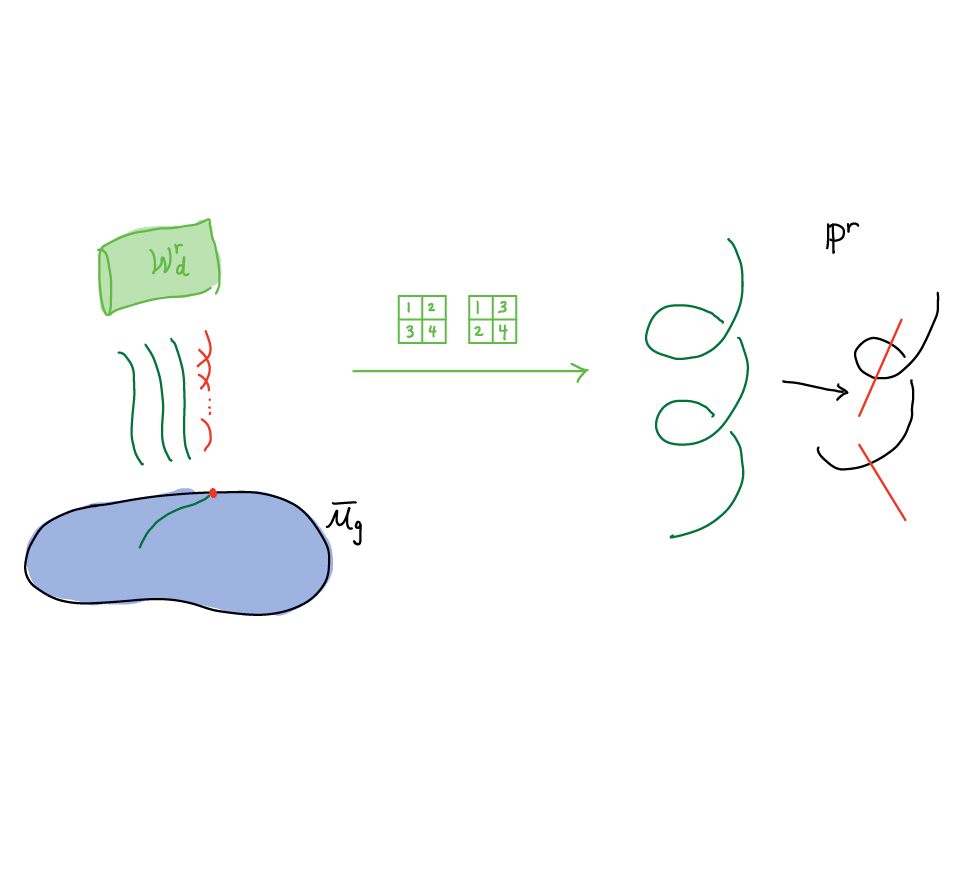
In the last few years, there have been extraordinary developments in many aspects of curve theory. Beginning with many examples in low genus, this summer school will introduce the participants to the background behind these developments in the following areas:
- moduli spaces of stable curves
- Brill–Noether theory
- the extrinsic geometry of the curves in projective space
We will also include an introduction to some open problems at the forefront of these active areas.
Updated on Jul 17, 2024 03:37 PM PDT -
Summer Graduate School Stochastic Quantization (SLMath)
Organizers: Massimiliano Gubinelli (University of Oxford), Martina Hofmanova (Universität Bielefeld), LEAD Hao Shen (University of Wisconsin-Madison), Lorenzo Zambotti (Sorbonne Université)
This summer school will familiarize students with the basic problems of the mathematical theory of Euclidean quantum fields. The lectures will introduce some of its prominent models and analyze them via the so called “stochastic quantization” methods, involving recently developed stochastic and PDE techniques. This is an area which is highly interdisciplinary combining ideas ranging from the theory of partial differential equations, to stochastic analysis, to mathematical physics. Our goal is to bring together students who are perhaps familiar with some but not all of these subjects and teach them how to integrate these different tools to solve cutting-edge problems of Euclidean quantum field theory.
Updated on Jul 01, 2024 03:11 PM PDT -
Summer Graduate School Koszul Duality in the Local Langlands Program (St. Mary's College)
Organizers: Clifton Cunningham (University of Calgary), LEAD Sarah Dijols (University of British Columbia)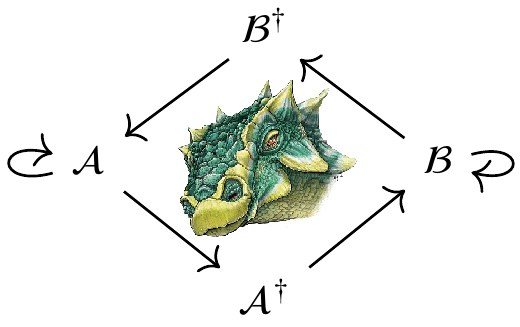
This summer school provides the mathematical background to recognize Koszul duality in representation theory. The school is especially oriented toward applications in the local Langlands program, with an emphasis on real groups. As Koszul duality patterns have been initially observed in the context of Hecke algebras, our school will also introduce the students to Hecke algebras and their categorifications.
Updated on Jul 11, 2024 10:27 AM PDT -
Summer Graduate School H-principle (Sendai, Japan)
Organizers: Emmy Murphy (Princeton University), Takashi Tsuboi (RIKEN Interdisciplinary Theoretical and Mathematical Sciences Program) The image of a large sphere isometrically embedded into a small space through a C^1 embedding. (Attributions: E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert)
The image of a large sphere isometrically embedded into a small space through a C^1 embedding. (Attributions: E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer, B. Thibert)This two week summer school, jointly organized by SLMath with RIKEN, will introduce graduate students to the theory of h-principles. After building up the theory from basic smooth topology, we will focus on more recent developments of the theory, particularly applications to symplectic and contact geometry, fluid dynamics, and foliation theory.
h-principles in smooth topology (Emmy Murphy)
Riemannian geometry and applications to fluid dynamics (Dominik Inauen)
Contact and symplectic flexibility (Emmy Murphy)
Foliation theory and diffeomorphism groups (Takashi Tsuboi)Updated on Jul 31, 2024 10:36 AM PDT -
Summer Graduate School Introduction to Quantum-Safe Cryptography (IBM Zurich)
Organizers: Jonathan Bootle (IBM Zürich Research Laboratory), Luca De Feo (IBM Zürich Research Laboratory)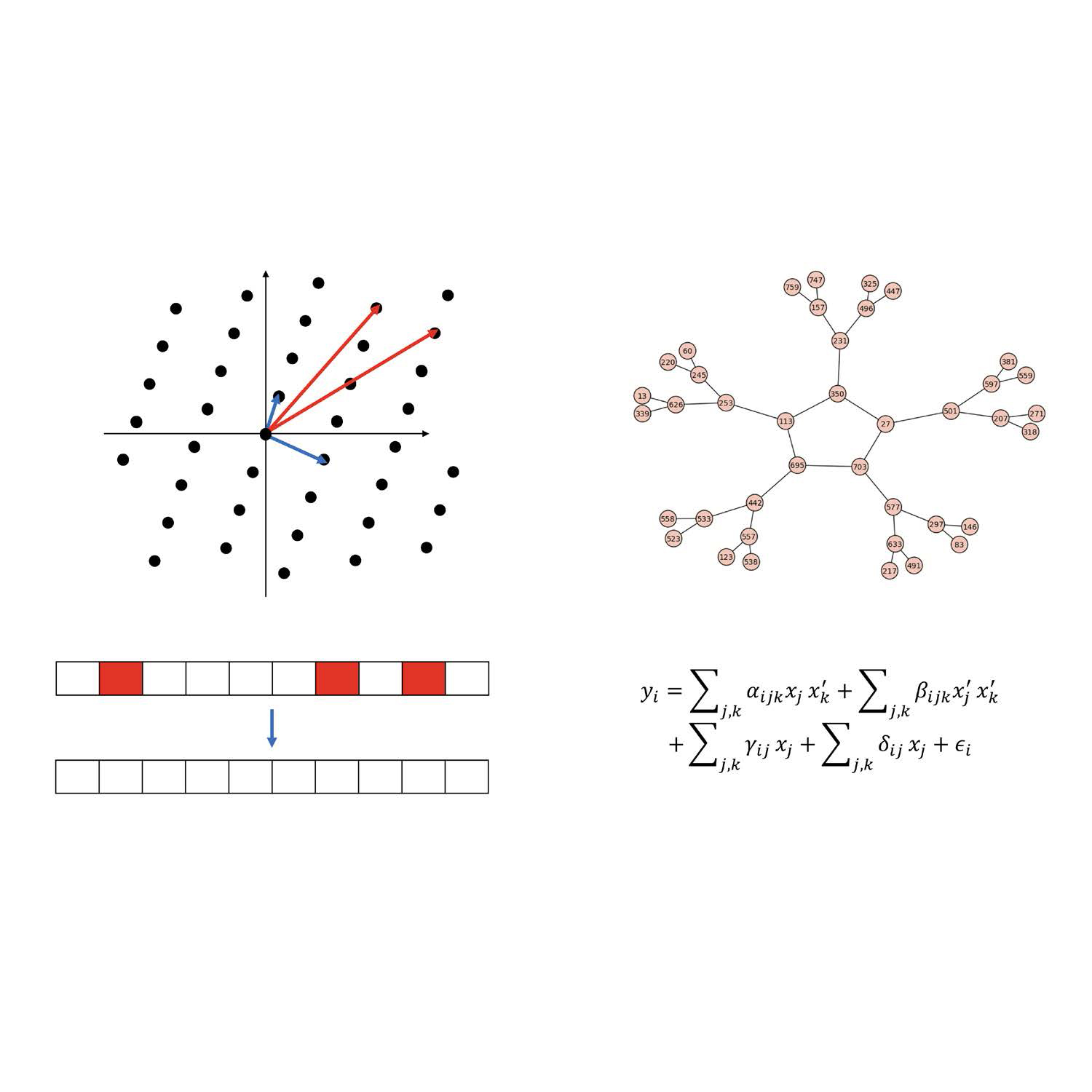
This two week summer school, jointly organized by SLMath with IBM Zurich, will introduce students to the mathematics and algorithms used in the design and analysis of quantum-safe cryptosystems. Each week will be dedicated to two of the four families of quantum-safe schemes.
Updated on Sep 26, 2024 11:17 AM PDT -
Summer Graduate School Special Geometric Structures and Analysis (St. Mary's College)
Organizers: Costante Bellettini (University College London), LEAD Eleonora Di Nezza (Institut de Mathématiques de Jussieu; École Normale Supérieure), Song Sun (Zhejiang University; University of California, Berkeley) a Calabi-Yau manifold
a Calabi-Yau manifoldThis summer school will serve as an introduction to the SLMath program "Special geometric structures and analysis". There will be two mini-courses: one in Geometric Measure theory and the other in Microlocal Analysis. The aim is to give the basic notions of two subjects also treated during the program.
Updated on Jun 27, 2024 01:13 PM PDT -
Summer Graduate School Particle interactive systems: Analysis and computational methods (SLMath)
Organizers: LEAD Irene M. Gamba (University of Texas, Austin), François Golse (Centre de Mathématiques Laurent Schwartz, École Polytechnique), LEAD Qin Li (University of Wisconsin-Madison), Chiara Saffirio (Universität Basel)
This summer school will focus on the introductory notions related to the passage of Newtonian and quantum many-body dynamics to kinetic collisional models of Boltzmann flow models arising in statistical sciences in connection to model reductions when continuum macro dynamics arises; and their numerical schemes associated to transport of kinetic processes in classical and data driven mean field dynamics incorporating recent tools from computational kinetics and data science tools. There will be two sets of lectures: “From Newton to Boltzmann to Fluid dynamics”, and “Kinetic collisional theory in mean field regimes: analysis, discrete approximations, and applications”. Each lecture series will be accompanied by a collaboration session, led by the lecturer and teaching assistants. The purpose of the collaboration sessions is to encourage and strengthen higher-level thinking of the materials taught in the lectures and to direct further reading for interested students. Interactive learning activities will be conducted. For example, students will be given problem sets associated with the lectures and will work in small groups to discuss concepts and/or find solutions to assigned problems. The students will also be encouraged to give oral or poster presentations on their solutions or other materials relevant to the course.
Updated on Jun 24, 2024 03:48 PM PDT