-
Program Complementary Program 2024-25
The Complementary Program has a limited number of memberships that are open to mathematicians whose interests are not closely related to the core programs; special consideration is given to mathematicians who are partners of an invited member of a core program.
Updated on Nov 03, 2023 03:25 PM PDT -
Summer Research in Mathematics 2025 Summer Research in Mathematics
SLMath's Summer Research in Mathematics (SRiM) program provides space, funding, and the opportunity for in-person collaboration to small groups of mathematicians, whose ongoing research may have been disproportionately affected by various obstacles including family obligations, professional isolation, or access to funding. Through this effort, SLMath aims to mitigate the obstacles faced by these groups, improve the odds of research project completion, and deepen their research experience. The ultimate goal of this program is to enhance the mathematical sciences as a whole by positively affecting the research and careers of all of its participants and assisting their efforts to maintain involvement in the research community.
Updated on Jun 06, 2025 10:10 AM PDT -
MSRI-UP MSRI-UP 2025: Quantitative Justice
Organizers: Alexander Diaz-Lopez (Villanova University), Maria Mercedes Franco (Queensborough Community College (CUNY)), Rebecca Garcia (Colorado College), Omayra Ortega (Sonoma State University), Candice Price (Smith College), LEAD Robin Wilson (Loyola Marymount University)The MSRI-UP summer program is designed to serve a diverse group of undergraduate students who would like to conduct research in the mathematical sciences.
In 2025, MSRI-UP will focus on Quantitative Justice. The research program will be led by Dr. Omayra Y. Ortega, Associate Professor in the Department of Mathematics at Sonoma State University.
Updated on Jun 16, 2025 08:29 AM PDT -
Summer Graduate School Geometry and Dynamics in Higher Rank Lie Groups (UC Berkeley)
Organizers: Richard Canary (University of Michigan), Sara Maloni (University of Virginia), Wenyu Pan (University of Toronto; University of Toronto), Cagri Sert (University of Warwick), LEAD Tengren Zhang (National University of Singapore)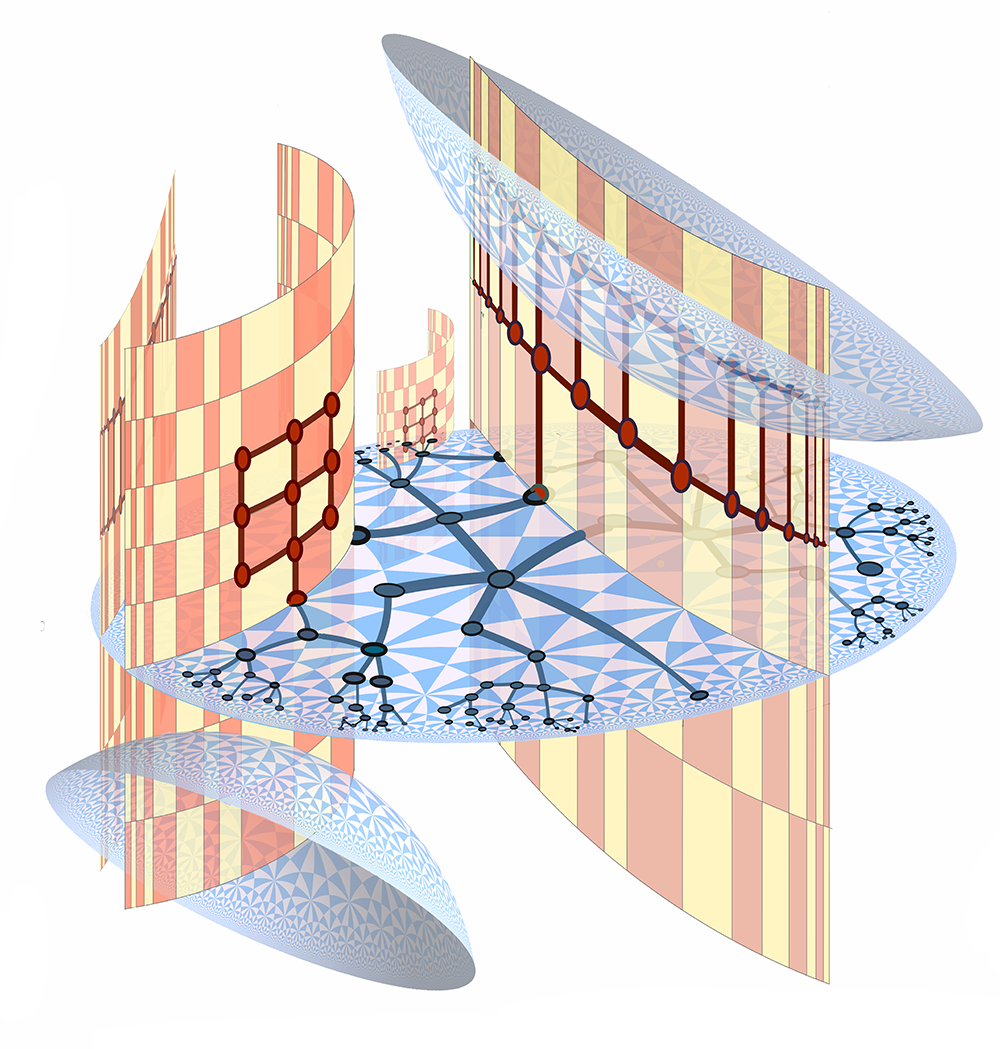 <p>Flats and hyperbolic planes in a higher rank symmetric space</p> Drawn by Steve Trettel.
<p>Flats and hyperbolic planes in a higher rank symmetric space</p> Drawn by Steve Trettel.Lie groups are central objects in modern mathematics; they arise as the automorphism groups of many homogeneous spaces, such as flag manifolds and Riemannian symmetric spaces. Often, one can construct manifolds locally modelled on these homogeneous spaces by taking quotients of their subsets by discrete subgroups of their automorphism groups. Studying such discrete subgroups of Lie groups is an active and growing area of mathematical research. The objective of this summer school is to introduce young researchers to a class of discrete subgroups of Lie groups, called Anosov subgroups.
Updated on Jul 23, 2025 03:36 PM PDT -
Summer Graduate School Topological and Geometric Structures in Low Dimensions (SLMath)
Organizers: LEAD Kenneth Bromberg (University of Utah), Kathryn Mann (Cornell University) <p>Laminations arise naturally in hyperbolic geometry and (pseudo-) Anosov flows [Image by Jeffrey Brock]</p>
<p>Laminations arise naturally in hyperbolic geometry and (pseudo-) Anosov flows [Image by Jeffrey Brock]</p>This school will serve as an introduction to the SLMath semester “Topological and Geometric Structures in Low-Dimensions”. The school consists of two mini-courses: one on Teichmüller Theory and Hyperbolic 3-Manifolds and the other on Anosov Flows on Geometric 3-Manifolds. Both topics lie at the interface of low-dimensional geometric topology (specifically, surfaces, foliations, and 3-manifolds) and low-dimensional dynamics. The first course will be targeted towards students who have completed the standard first year graduate courses in geometry, topology, and analysis while the second course will geared towards more advanced students who are closer to beginning research. However, we expect that all students will benefit from both courses.
Updated on Jul 25, 2025 10:18 AM PDT
-
Program Kinetic Theory: Novel Statistical, Stochastic and Analytical Methods
Organizers: Laurent Desvillettes (Université Paris Cité), Irene M. Gamba (University of Texas, Austin), François Golse (Centre de Mathématiques Laurent Schwartz, École Polytechnique), Cyril Imbert (École Normale Supérieure), LEAD Pierre-Emmanuel Jabin (Pennsylvania State University), Qin Li (University of Wisconsin-Madison), Chiara Saffirio (Universität Basel), Weiran Sun (Simon Fraser University), Lexing Ying (Stanford University) Top: Neutrino interactions and neutrino-atom interactions. Bottom: Collision of two "waves"
Top: Neutrino interactions and neutrino-atom interactions. Bottom: Collision of two "waves"The focus of the proposed program is on so-called kinetic equations, describing the evolution of the of many-particle interacting systems. These models have the form of statistical flows, with their solutions being either a single or multiple point probability density functions or measures, supported in a space of attributes. The attributes are problem-dependent and can be molecular velocity, energy, opinion, wealth, and many others. The flow then predicts the evolution of the probability measure in time, position in space, and the interchanging of the particles' states by the transition probability.
The program will strive to give an overview of the novel mathematical tools used in kinetic theory through a broad range of classical and more recent applications.
Updated on Jul 23, 2025 01:24 PM PDT -
Program Recent Trends in Stochastic Partial Differential Equations
Organizers: Sandra Cerrai (University of Maryland), Yu Gu (University of Maryland), Massimiliano Gubinelli (University of Oxford), Davar Khoshnevisan (University of Utah), Andrea Nahmod (University of Massachusetts, Amherst), Hao Shen (University of Wisconsin-Madison), LEAD Lorenzo Zambotti (Sorbonne Université)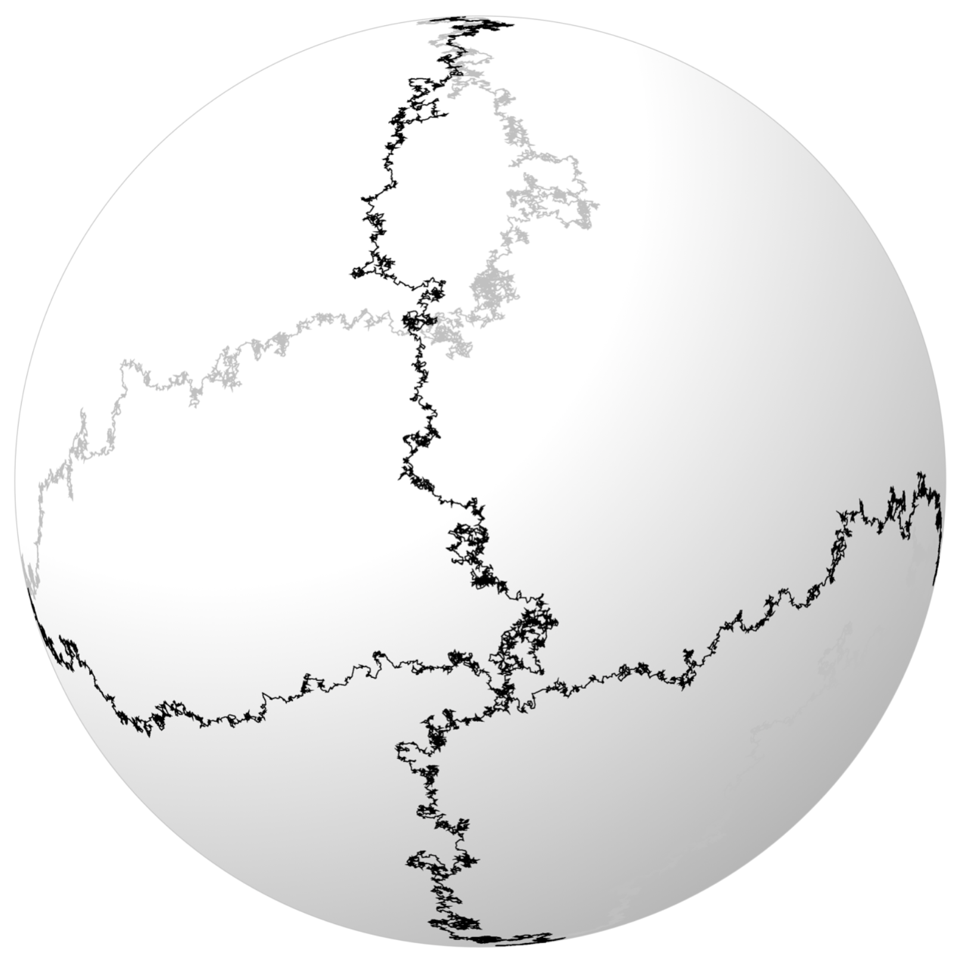 Solution to the geometric stochastic heat equation on the sphere at a fixed time
Solution to the geometric stochastic heat equation on the sphere at a fixed timeThe topic Singular Stochastic Partial Differential Equations (singular SPDE) has rapidly grown to be an active research area at the interface of Stochastic Analysis and PDEs on one hand, and Mathematical Physics on the other hand. During this decade we have witnessed a series of tremendous breakthroughs in the solution theories of SPDEs, universality problems, large-scale asymptotic behaviors of solutions, and foundational relations with quantum field theories and geometry. Many long-standing problems have been resolved via newly developed methods – notably the theories of regularity structures and paracontrolled distributions – and deep connections with other fields are quickly emerging.
It is a natural time to convene a large-scale semester program.
Updated on Jul 09, 2024 04:18 PM PDT -
Program Complementary Program 2025-26
The Complementary Program has a limited number of memberships that are open to mathematicians whose interests are not closely related to the core programs; special consideration is given to mathematicians who are partners of an invited member of a core program.
Updated on Dec 03, 2024 03:13 PM PST -
Workshop Pathways Workshop: Kinetic Theory & Stochastic Partial Differential Equations
Organizers: LEAD Raluca Balan (University of Ottawa), François Golse (Centre de Mathématiques Laurent Schwartz, École Polytechnique), Qin Li (University of Wisconsin-Madison), Xiaoming Song (Drexel University), Rongchan Zhu (Beijing Institute of Technology)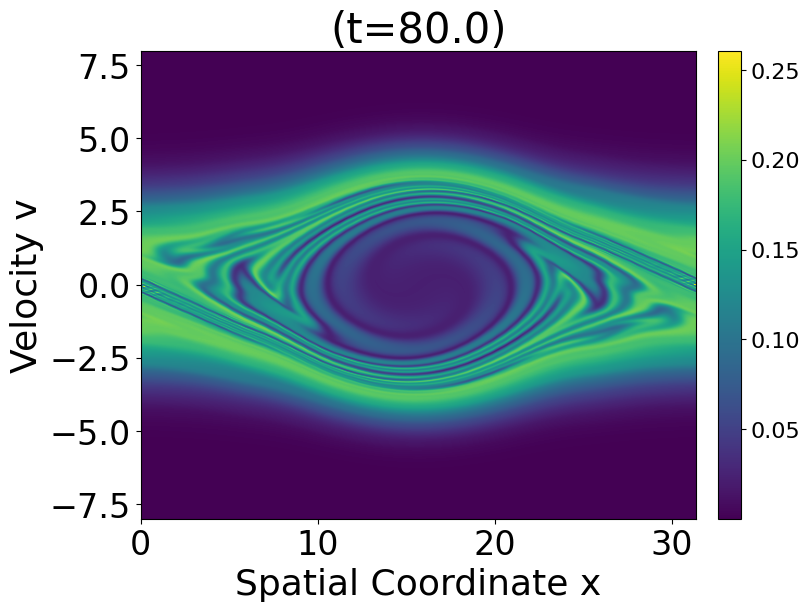
The Pathways workshop will bring together leading experts working at the intersection of kinetic theory and stochastic partial differential equations (SPDEs).
Updated on Jul 18, 2025 03:36 PM PDT -
Workshop Introductory Workshop: Kinetic Theory & Stochastic Partial Differential Equations
Organizers: Davar Khoshnevisan (University of Utah), Qin Li (University of Wisconsin-Madison), LEAD Konstantin Matetski (Columbia University; Michigan State University), Andrea Nahmod (University of Massachusetts, Amherst), Chiara Saffirio (Universität Basel), Xiangchan Zhu (Chinese Academy of Sciences)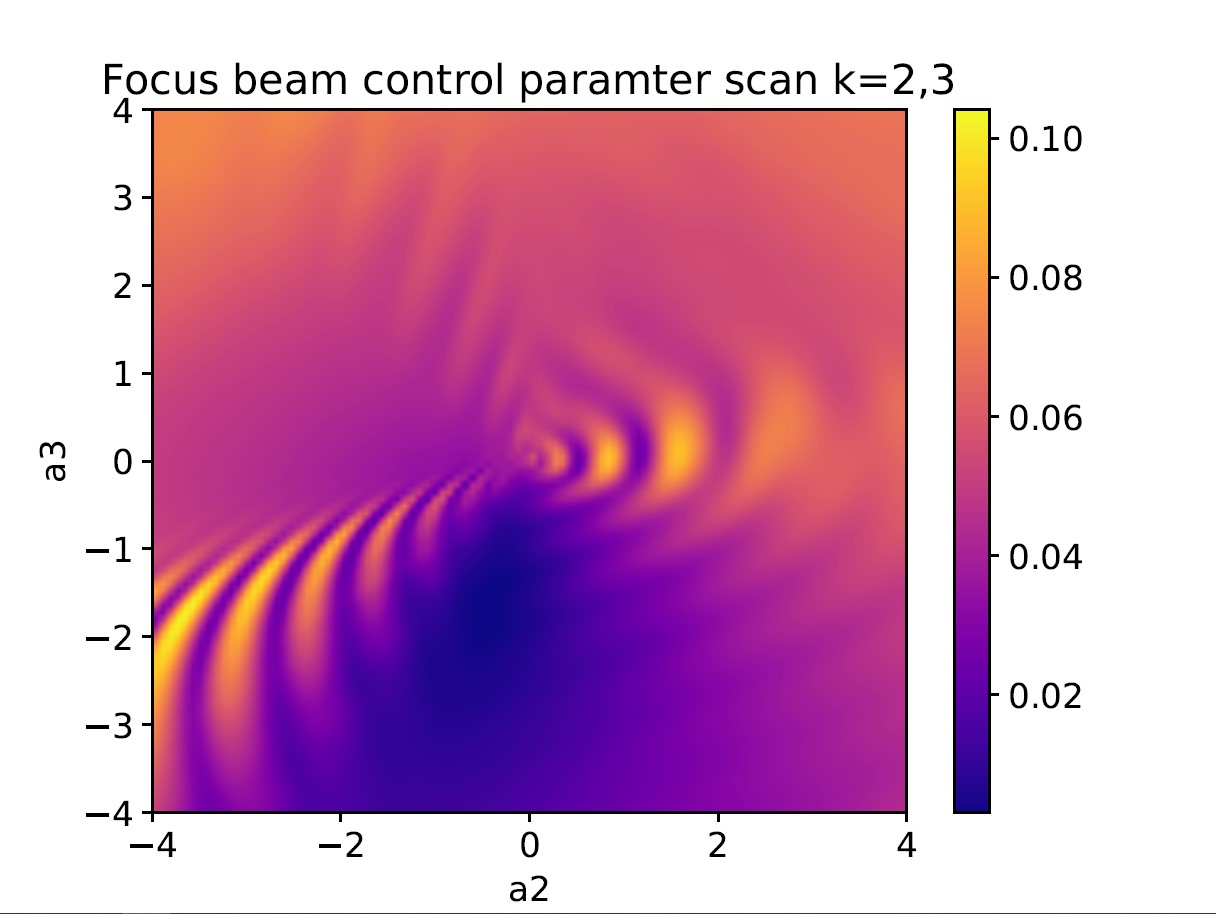 Parameter scan for deploying external electric field to control two-stream instability for Vlasov-Poisson.
Parameter scan for deploying external electric field to control two-stream instability for Vlasov-Poisson.The goal of the workshop is to introduce non-experts to two active research areas: kinetic theory and stochastic partial differential equations. Kinetic theory studies the properties of interacting particle systems modeling various processes in non-equilibrium statistical mechanics. Stochastic partial differential equations describe dynamics subjected to random noises. The methods from the two areas complement each other in studies of the phenomena arising in physics, economics, life sciences, etc.
Updated on May 08, 2025 04:43 PM PDT -
Workshop Kinetic Theory: Novel Statistical, Stochastic and Analytical Methods
Organizers: Irene M. Gamba (University of Texas, Austin), LEAD Weiran Sun (Simon Fraser University) Top: Neutrino interactions and neutrino-atom interactions. Bottom: Collision of two "waves"
Top: Neutrino interactions and neutrino-atom interactions. Bottom: Collision of two "waves"This workshop will explore the latest advances in kinetic theory and stochastic particle dynamics in mean field regimes, covering both classical themes and emerging areas. Topics will include the derivation of kinetic type equations from particle and plasma systems, state-of-the-art numerical methods, studies of multiscale phenomena, and the applications of kinetic equations in physics, chemistry, computer sciences appearing in life sciences, social sciences, and machine learning. This workshop will offer an exciting opportunity to connect researchers from all stages and sub-areas and spark new ideas.
Updated on Jul 11, 2025 04:27 PM PDT -
Workshop Recent Trends in Stochastic Partial Differential Equations
Organizers: Sandra Cerrai (University of Maryland), LEAD Ilya Chevyrev (University of Edinburgh), Yu Deng (University of Chicago), Martina Hofmanova (Universität Bielefeld)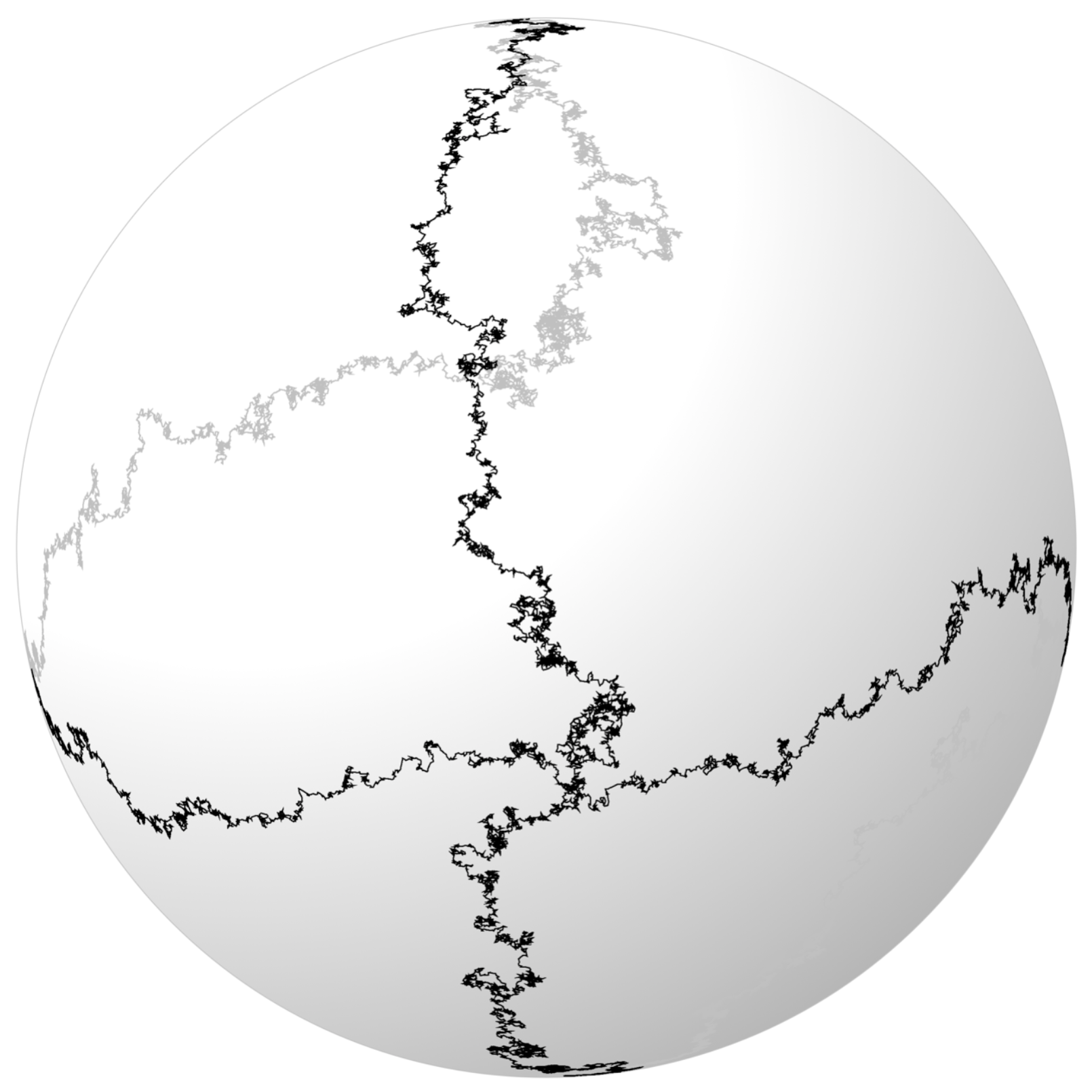 The motion of a random string.
The motion of a random string.The workshop aims to bring together researchers working on different facets of stochastic PDEs. The field of stochastic PDEs has seen many new techniques recently appear to tackle different problems, including renormalization, large scale and long-time behaviours, stochastic fluid dynamics, and homogenization. The goal of the workshop is to facilitate discussions and allow different communities to engage with one another one.
Updated on Jul 11, 2025 01:03 PM PDT -
Workshop Revisiting Fundamental Problems Workshop: Infinite-Dimensional Division Algebras - Algebraicity and Freeness
Organizers: Agatha Atkarskaya (The Hebrew University of Jerusalem), Jason Bell (University of Waterloo), LEAD Be'eri Greenfeld (University of California, San Diego), Susan Sierra (University of Edinburgh), LEAD James Zhang (University of Washington) Tribute to Hamilton's graffiti of the Quaternion Division Algebra, County Dublin, Ireland. Photo: Professor Peter Gallagher, Director Dublin Institute for Advanced Studies Dunsink Observatory (courtesy DIAS)
Tribute to Hamilton's graffiti of the Quaternion Division Algebra, County Dublin, Ireland. Photo: Professor Peter Gallagher, Director Dublin Institute for Advanced Studies Dunsink Observatory (courtesy DIAS)Infinite-dimensional division algebras are essential in noncommutative algebra and noncommutative algebraic geometry, yet they have remained cryptic and largely unclassified. This workshop will address three key classical open problems concerning them: the Kurosh Problem, the Free Subalgebra Problem and Artin's Conjecture. We will review decades of progress on these wide-open problems and emphasize novel techniques and emerging theories and concepts that show promise in facilitating breakthroughs.
Updated on Jul 15, 2025 10:08 AM PDT -
Program Geometry and Dynamics for Discrete Subgroups of Higher Rank Lie Groups
Organizers: Martin Bridgeman (Boston College), LEAD Richard Canary (University of Michigan), Amir Mohammadi (University of California, San Diego), LEAD Hee Oh (Yale University), Maria Beatrice Pozzetti (Università di Pisa; Università di Bologna), Jean-François Quint (CNRS - Université de Montpellier)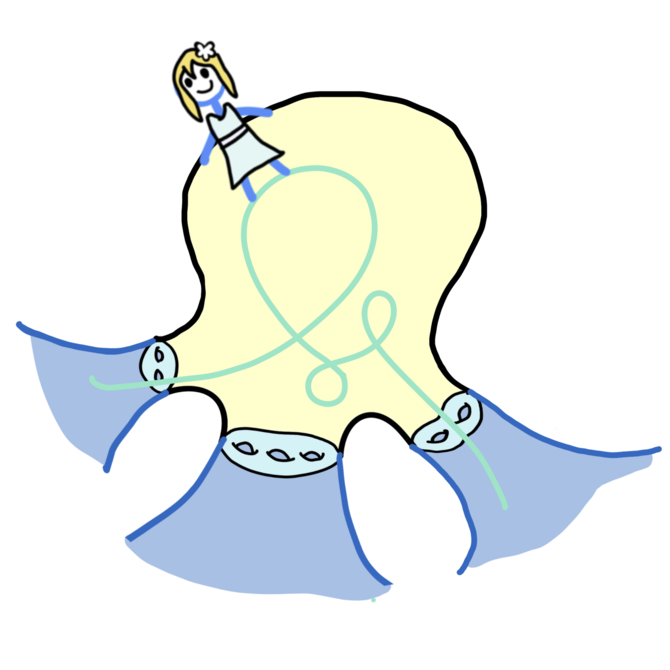 <p>This figure depicts dynamics of flows on convex cocompact hyperbolic 3-manifolds; where the girl is a traveller along a horocycle.</p>
<p>This figure depicts dynamics of flows on convex cocompact hyperbolic 3-manifolds; where the girl is a traveller along a horocycle.</p>This research program will bring together two intellectual communities that have made significant advances in the study of discrete subgroups of higher rank semisimple Lie groups: the homogeneous dynamics community and the community studying geometric structures and Anosov groups.
Updated on Jul 16, 2025 09:04 AM PDT -
Program Topological and Geometric Structures in Low Dimensions
Organizers: Ian Agol (University of California, Berkeley), Kenneth Bromberg (University of Utah), Sebastian Hensel (LMU München), Christopher Leininger (Rice University), Kathryn Mann (Cornell University), LEAD Yair Minsky (Yale University), Rachel Roberts (Washington University in St. Louis) The stable and unstable foliations near a singular orbit of a pseudo- Anosov flow in 3 dimensions. Courtesy Michael Landry.
The stable and unstable foliations near a singular orbit of a pseudo- Anosov flow in 3 dimensions. Courtesy Michael Landry.Low dimensional topology is a meeting place for many objects and ideas from diverse areas of mathematics, including foliation theory, geometry, and smooth and conformal dynamics. For instance, many foliations on 3-manifolds admit transverse flows, connecting (local) leafwise homeomorphisms to flow dynamics and the mapping class groups of the leaves. Leafwise conformal or hyperbolic structures can be approached through Teichmüller theory, and connect again to one-dimensional dynamics through "universal circles" organizing compactifications of all the leaves or of the flow space. Many of these ideas originate in work of Thurston but in recent years have diverged and are ripe for reconnection.
The program will bring together experts in all these fields together with younger researchers, who together can form new connections and open new areas for exploration.Updated on Jul 16, 2025 09:04 AM PDT -
Workshop Pathways Workshop: Topological and Geometric Structures in Low Dimensions & Geometry and Dynamics for Discrete Subgroups of Higher Rank Lie Groups
Organizers: Martin Bridgeman (Boston College), Lei Chen (University of Chicago; University of Maryland), Beibei Liu (Ohio State University), Maria Beatrice Pozzetti (Università di Pisa; Università di Bologna), Rachel Roberts (Washington University in St. Louis), Jing Tao (University of Oklahoma)
This workshop features a series of invited talks by experts across the fields of low-dimensional topology, homogeneous dynamics, and the geometry of symmetric spaces. Spanning all career stages, the event aims to foster a collaborative and supportive environment, particularly for early-career mathematicians, encouraging engagement, learning, and exploration in a welcoming academic setting.
Updated on Jun 10, 2025 11:05 AM PDT -
Workshop Introductory Workshop: Topological and Geometric Structures in Low Dimensions & Geometry and Dynamics for Discrete Subgroups of Higher Rank Lie Groups
Organizers: Federica Fanoni (University of Warwick), Steven Frankel (Washington University), LEAD Yair Minsky (Yale University), Amir Mohammadi (University of California, San Diego), Andrés Sambarino (Université de Paris VII (Denis Diderot) et Université de Paris VI (Pierre et Marie Curie)), Barbara Schapira (Université de Picardie (Jules Verne)), Genevieve Walsh (Tufts University)
The joint introductory workshop for the programs in Geometry and Dynamics for Discrete Subgroups of Higher Rank Lie Groups and Topological and Geometric Structures in Low Dimensions will feature lectures introducing subjects of interest to both programs, including Teichmuller Theory, geometry in higher rank, foliations and flows, Anosov groups and thermodynamic formalism, mapping class groups, counting and equidistribution, and related topics. Minicourses will be targeted at early career researchers as well as specialists looking to find connections between the different subjects.
Updated on Jul 23, 2024 02:18 PM PDT -
Workshop Recent Progress in Topological and Geometric Structures in Low Dimensions
Organizers: Kenneth Bromberg (University of Utah), Sergio Fenley (Florida State University), Autumn Kent (University of Wisconsin-Madison), LEAD Kathryn Mann (Cornell University), Kasra Rafi (University of Toronto)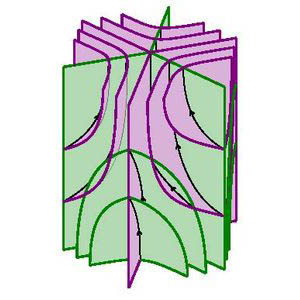 Foliations around a pseudo-Anosov singularity (Image credit: Chi Cheuk Tsang)
Foliations around a pseudo-Anosov singularity (Image credit: Chi Cheuk Tsang)This workshop will bring together ideas from diverse areas of mathematics that meet in the setting of geometry and topology in low dimensions. This includes the study of flows, foliations, and fibrations of three-manifolds and the related study of geometry (e.g. hyperbolic or conformal structures) of the manifolds and of the leaves or fibers, and their mapping class groups. This is a rich and interconnected area and many adjacent topics will also be featured.
Updated on Jul 15, 2025 10:39 AM PDT -
Workshop Homogeneous Dynamics and Anosov Representations
Organizers: LEAD Marc Burger (ETH Zürich), Simion Filip (University of Chicago), Ursula Hamenstädt (Rheinische Friedrich-Wilhelms-Universität Bonn), Fanny Kassel (Institut des Hautes Études Scientifiques (IHES)), Hee Oh (Yale University), Jean-François Quint (CNRS - Université de Montpellier) Limit set of an Anosov representation
Limit set of an Anosov representationThis workshop will focus on recent advances on geometric and dynamical approaches to the study of discrete subgroups of higher rank Lie groups and their deformation spaces. The goal will be to present results and exchange ideas from different areas of mathematics, and we hope to create bonds between several different mathematical communities.
Updated on Jul 15, 2025 10:47 AM PDT -
Summer Graduate School Séminaire de Mathématiques Supérieures 2026: Universal Statistics in Number Theory (Montréal, Canada)
Organizers: Louis-Pierre Arguin (University of Montreal), Chantal David (Concordia University), Andrew Granville (Université de Montréal), Wei Ho (Institute for Advanced Study), Dimitris Koukoulopoulos (Université de Montréal), Matilde Lalin (Université de Montréal), Carlo Pagano (Concordia University), Frank Thorne (University of South Carolina)One of the hottest topics in analytic number theory involves the use of statistics and probability in understanding different aspects of algebraic and analytic number theory, through various new lenses. This is reflected in some of the most exciting number theory research of the last few years (for example, of Bhargava, of Ellenberg and Venkatesh, of Alexander Smith, of Sawin and Wood, of Adam Harper, of Koukoulopoulos and Maynard, of Helfgott and Radziwill, of Pilatte,....). As a consequence the CRM will host a thematic semester Mar 2-July 3, 2026 on these topics involving some of the world leaders in the subject. Since this new area can roughly be split in two into Algebraic and Analytic, we will focus for two months on each, with the SMS school placed in the middle. The 2026 SMS will introduce junior mathematicians to important trends in number theory.
Updated on Jul 23, 2025 01:35 PM PDT -
Summer Graduate School Percolation and lattice models of statistical physics (Columbia University)
Organizers: Roland Bauerschmidt (New York University, Courant Institute), Tom Hutchcroft (California Institute of Technology) <p>The five largest clusters in critical site percolation on a large three-dimensional box</p>
<p>The five largest clusters in critical site percolation on a large three-dimensional box</p>Percolation and spin models such as the Ising model have a history that goes back over 100 years. The subject has taken a central role in probability theory over the last few decades, in particular through interactions with various other areas of mathematics. These include graph theory, theoretical
computer science, statistical physics, quantum field theory, complex analysis, partial differential equations, and geometric group theory. Through examples, the summer school aims to illustrate some of the successful techniques and ideas in the subject area.Updated on Jul 23, 2025 01:34 PM PDT -
Summer Graduate School Geometric Measure Theory (SLMath)
Organizers: Camillo De Lellis (Institute for Advanced Study), Guido De Philippis (Hausdorff Research Institute for Mathematics, University of Bonn)
The school will consist of three interrelated courses, aimed to introduce the main concepts in Geometric Measure Theory.
(1) Sets and measure in the Euclidean space, Guido De Philippis (Courant Institute of Mathematical Sciences)
(2) Theory of currents, Annalisa Massaccesi (University of Padua)
(3) Allard regularity theory, Camillo De Lellis (Institute of Advanced Study)Updated on Jul 18, 2025 09:50 AM PDT -
Summer Graduate School ICTP-INdAM-SLMath School: Mathematics For Machine Learning (Trieste, Italy)
Organizers: Claudio Arezzo (Abdus Salam International Centre for Theoretical Physics), Jean Barbier (Abdus Salam International Centre for Theoretical Physics), Filippo Bracci (Università di Roma Tor Vergata), LEAD Domenico Marinucci (Università di Roma Tor Vergata), Cristina Trombetti (CSEF and Università degli Studi di Napoli Federico II)The aim of this summer school is to provide an introduction to theoretical ideas that have been developed with the objective of understanding machine learning methods and their domain of applicability. The focus will be on proof technique and general mathematical tools. The lecturers are two worldwide experts in the area and the material is regularly taught in Mathematics and Statistics Departments of the top world Universities.
Updated on Jul 23, 2025 02:08 PM PDT -
Summer Graduate School Random growth models, phase separation and Hamilton-Jacobi PDE (UC Berkeley)
Organizers: Alan Hammond (University of California, Berkeley), Fraydoun Rezakhanlou (University of California, Berkeley)Models of random growth and of the separation of phases occurring when one substance is suspended in another often evince universal features, in which scaling exponents are shared among a broad class of such models. A foothold for understanding such features is often offered by studying a few special models that are exactly solvable, which means that exact formulas of algebraic or integrable origin are available. Showing that a broader range of models also have the features is a task that may rely on a range of robust probabilistic or geometric tools. The summer school will offer an introduction to random growth and phase separation, with an emphasis on tools that offer the prospect of proving universality for a wider class of models.
Updated on Jul 22, 2025 03:02 PM PDT -
Summer Graduate School Mathematics of Generative Models (SLMath)
Organizers: Jianfeng Lu (Duke University), Eric Vanden-Eijnden (New York University, Courant Institute) <p>Artificial image generation by flow-based generative models starting from noise</p>
<p>Artificial image generation by flow-based generative models starting from noise</p>The overarching goal of this summer school is to expose students to the latest developments in the mathematics of generative models. Our ultimate goal is to teach them how to conduct research in this exciting area in machine learning and use their knowledge to make contributions to applied mathematics using these new tools.
Updated on Jul 18, 2025 09:49 AM PDT -
Summer Graduate School SLMath-Oxford-OIST School: Analysis of Partial Differential Equations (Okinawa, Japan)
Organizers: Ugur Abdulla (Okinawa Institute of Science and Technology), Gui-Qiang Chen (University of Oxford)This two week summer school, jointly organized by SLMath with OIST, will offer the following two mini-courses:
- Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
This course will present some recent developments in the theory of divergence-measure fields via measure-theoretic analysis and its applications to the analysis of nonlinear PDEs of conservative form – nonlinear conservation laws. - Perron’s method and Wiener-type criteria in the potential theory of elliptic and parabolic PDEs
This course will present some recent developments precisely characterizing the regularity of the point at ∞ for second order elliptic and parabolic PDEs and broadly extending the role of the Wiener test in classical analysis.
Updated on Jul 23, 2025 01:38 PM PDT - Measure-theoretical analysis, divergence-measure fields, and nonlinear PDEs of divergence form
-
Summer Graduate School Singularities in commutative algebra through cohomological methods (SLMath)
Organizers: Benjamin Briggs (Imperial College, London), Eloísa Grifo (University of Nebraska), Josh Pollitz (Syracuse University) <p>Homotopy measures how spheres can be tangled in spaces; the logo shows a sphere tangled in a grove of California redwoods<br />The background painting is “Giant Redwood Trees of California” by Albert Bierstadt in 1874</p>
<p>Homotopy measures how spheres can be tangled in spaces; the logo shows a sphere tangled in a grove of California redwoods<br />The background painting is “Giant Redwood Trees of California” by Albert Bierstadt in 1874</p>The goal of this school will be to introduce students to several powerful cohomological tools that were brought to commutative algebra by Avramov in the 80s and 90s: Lie algebra methods from homotopy theory, and support theoretic methods from the representation theory of finite groups. These tools have have seen a huge array of applications that continue to grow, with several major developments in recent years, opening new connections to algebraic topology, noncommutative algebraic geometry, and representation theory.
Updated on Jul 18, 2025 09:50 AM PDT -
Summer Graduate School Moduli of Varieties (SLMath)
Organizers: Kenneth Ascher (University of California, Irvine), Dori Bejleri (University of Maryland), Kristin DeVleming (University of California, San Diego)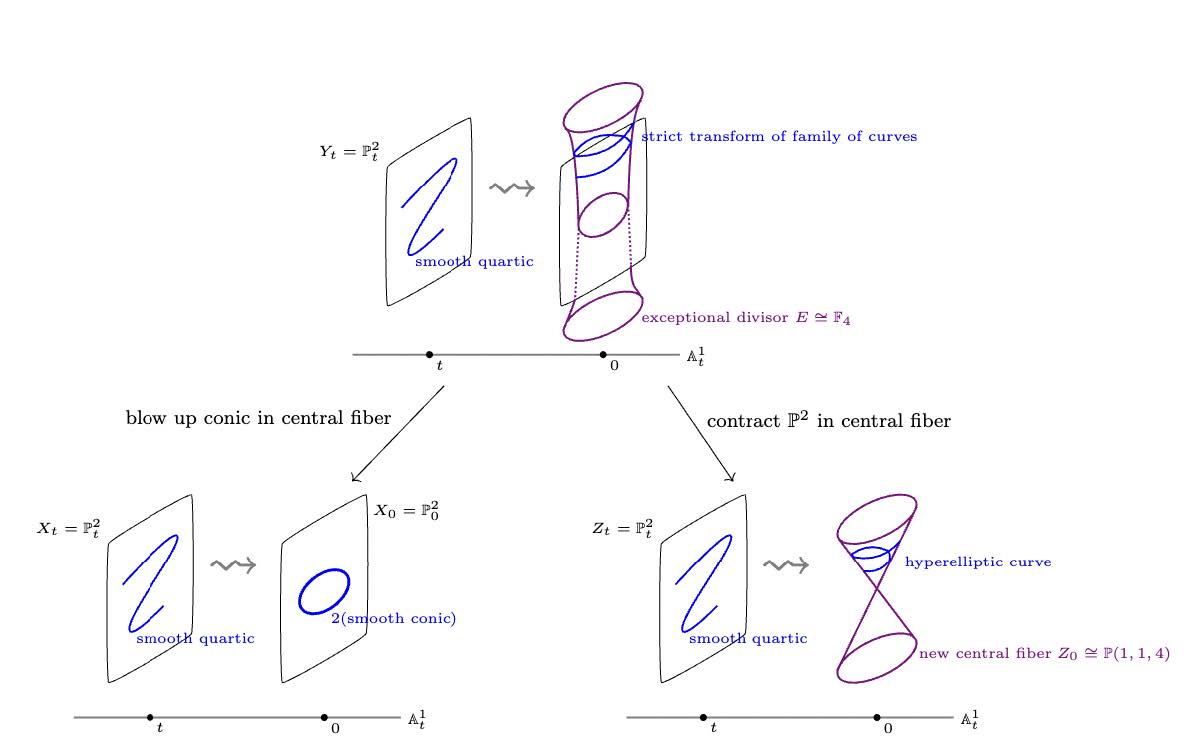 <p>A wall-crossing in a moduli problem</p>
<p>A wall-crossing in a moduli problem</p>One of the central problems in algebraic geometry is to classify so-called algebraic varieties: geometric shapes cut out by polynomial equations. Algebraic varieties are parametrized by certain moduli spaces (roughly: parameter spaces whose points correspond to these different varieties). The geometry of these moduli spaces encodes the ways of continuously deforming these shapes. Furthermore, classification questions for algebraic varieties often boil down to understanding the geometry of these moduli spaces. In the past few years, powerful new tools have been developed in moduli theory, especially for higher dimensional varieties – those which are of complex dimension at least two. The goal of this summer school is to provide an introduction to many of these recently emerging breakthroughs to enable graduate students to begin working in this area. The program will be motivated and often guided by examples and is intended to be accessible to a wide variety of students
Updated on Jul 18, 2025 09:51 AM PDT -
Program Representation Theory Under the Influence of Quantum Field Theory
Organizers: David Ben-Zvi (University of Texas, Austin), LEAD Tudor Dimofte (University of Edinburgh), Iva Halacheva (Northeastern University), LEAD Joel Kamnitzer (University of Toronto), Pavel Safronov (University of Edinburgh), Peng Shan (Tsinghua University) <p>Illustrated by Rok Gregoric</p>
<p>Illustrated by Rok Gregoric</p>The upcoming SLMath program is organized around key themes of “higher” quantization and mirror symmetry as they impact and elucidate a wide variety of questions in representation theory. The program will bring together experts and young researchers from algebra, geometry, physics and number theory to help develop and disseminate this unified vision of a rapidly evolving field, exploring the mathematical consequences of the examples, structures, and dualities discovered in physics.
Updated on Jul 16, 2025 09:07 AM PDT -
Program Motivic Homotopy Theory: Connections and Applications
Organizers: Aravind Asok (University of Southern California), Adrien Dubouloz (Institut de Mathématiques de Bourgogne), Elden Elmanto (University of Toronto, Scarborough; Harvard University), Daniel Isaksen (Wayne State University), Paul-Arne Oestvær (Università di Milano), Anand Sawant (Tata Institute of Fundamental Research), Kirsten Wickelgren (Duke University), Maria Yakerson (Institut de Mathématiques de Jussieu - Paris Rive Gauche)Tremendous progress has been made using motivic techniques in geometric questions for affine algebraic varieties, especially those involving algebraic vector bundles. Computations in classical algebraic topology have been improved by motivic techniques, e.g., related to the problem of computing homotopy groups of spheres. Moreover, the theory has identified new structures of interest in arithmetic situations. Transformative recent progress in motivic homotopy theory has only broadened the scope for potential applications of motivic techniques, as well as new avenues of interaction with other areas of mathematics. This program will build on previous successes, explaining the tools that have been developed and how to use them, analyzing questions of the sort described above and identifying new domains where motivic techniques will be successful.
Updated on Jul 16, 2025 09:24 AM PDT -
Workshop Pathways Workshop: Representation Theory Under the Influence of Quantum Field Theory & Motivic Homotopy Theory
Organizers: Ana Balibanu (Louisiana State University), Asilata Bapat (Australian National University), Teena Gerhardt (Michigan State University), Iva Halacheva (Northeastern University), Padmavathi Srinivasan (Boston University), Kirsten Wickelgren (Duke University)Updated on Jun 10, 2025 11:08 AM PDT -
Workshop Introductory Workshop: Representation Theory Under the Influence of Quantum Field Theory & Motivic Homotopy Theory
Organizers: David Ben-Zvi (University of Texas, Austin), Elden Elmanto (University of Toronto, Scarborough; Harvard University), Iva Halacheva (Northeastern University), Pavel Safronov (University of Edinburgh), Anand Sawant (Tata Institute of Fundamental Research), Peng Shan (Tsinghua University), Craig Westerland (University of Minnesota Twin Cities), Maria Yakerson (Institut de Mathématiques de Jussieu - Paris Rive Gauche)Updated on Jun 10, 2025 11:07 AM PDT -
Workshop Geometric Representation Theory and 3d Mirror Symmetry
Organizers: Tudor Dimofte (University of Edinburgh), Joel Kamnitzer (University of Toronto), Sam Raskin (University of Texas, Austin), Peng Shan (Tsinghua University), LEAD Benjamin Webster (University of Waterloo) Image by Elliot Kienzle
Image by Elliot KienzleThis workshop will bring together theoretical physicists, representation theorists, algebraic geometers and symplectic geometers interested the connections between quantum field theory and geometric representation theory. The main topics to be discussed are mathematical aspects of 2d, 3d and 4d supersymmetric field theories, such as: topological twists and the resulting Higgs and Coulomb branches, relations to quantization and categorification, representations of vertex operator algebras, connections to enumerative geometry and quantum K-theory and elliptic cohomology, relations to knot homology and, finally, connections to the (relative) geometric Langlands program.
Updated on Jul 15, 2025 04:27 PM PDT -
Program New Trends in Tropical Geometry
Organizers: Pierrick Bousseau (University of Georgia), Melody Chan (Brown University), Ilia Itenberg (Institut de Mathématiques de Jussieu - Paris Rive Gauche), Hannah Markwig (Eberhard-Karls-Universität Tübingen), LEAD Kris Shaw (University of Oslo) Tropical surfaces. Images courtesy of Lars Allermann.
Tropical surfaces. Images courtesy of Lars Allermann.Tropical geometry can be viewed as a degenerate version of algebraic geometry,where the role of algebraic varieties is played by certain polyhedral complexes. As the degeneration process, called tropicalization, preserves many fundamental properties, tropical geometry provides important bridges and an exchange of methods between algebraic geometry, symplectic geometry and convex geometry; these links have been extremely fruitful and gave rise to remarkable results during the last 20 years. The main focus of the program will be on the most significant recent developments in tropical geometry and its applications. The following topics are particularly influential in the area and will be central in the program:
- real aspects of tropical geometry;
- tropical mirror symmetry and non-Archimedean geometry;
- tropical phenomena in symplectic geometry;
- matroids, combinatorial and algebraic aspects;
- tropical moduli spaces;
- tropical geometry and A1-homotopy theory.
Updated on Jul 10, 2025 09:28 AM PDT -
Program Algebraic Combinatorics
Organizers: Sara Billey (University of Washington), LEAD Sylvie Corteel (Université de Paris VII (Denis Diderot); University of California, Berkeley), Philippe Di Francesco (University of Illinois at Urbana-Champaign), Cynthia Vinzant (University of Washington), Lauren Williams (Harvard University) Picture of an amplituhedron
Picture of an amplituhedronAlgebraic combinatorics is an area of mathematics that employs methods in abstract algebra in combinatorial contexts, and that uses combinatorial methods to approach problems in algebra. Some important topics are symmetric functions, Young tableaux, matroids, Coxeter combinatorics. There are links to computer algebra (sage-combinat), number theory (L-functions), representation theory, and mathematical physics through Macdonald processes and integrability. The work on the totally positive Grassmannian also gave rise to beautiful results in mathematical physics: for example KP solitons and Scattering Amplitudes. Schubert calculus is an important part of algebraic combinatorics and is now at the frontier with k-Schur functions, which first came up in the theory of Macdonald polynomials.
Updated on Jul 10, 2025 09:39 AM PDT -
Program Inverse Problems and Applications
Organizers: Fioralba Cakoni (Rutgers University), Maarten de Hoop (Rice University), Anna Gilbert (Yale University), Katya Krupchyk (University of California, Irvine), Matti Lassas (University of Helsinki), LEAD Gunther Uhlmann (University of Washington)
Inverse problems (IP) arise in all fields of science and technology where a cause for an observed or desired effect is sought. In the last 50 years or so there has been substantial progress in the mathematical understanding of these problems but many questions remain open. The mathematics of these problems involves many areas in Mathematics including PDE, differential geometry, integral geometry, probability, statistics, complex analysis, numerical analysis, mathematical physics, data science, etc. Since the 2010 program at the then-Mathematical Sciences Research Institute (now Simons Laufer Mathematical Sciences Institute), there has been significant progress in inverse problems; many of the advances can be traced back to that program. However, there are still deep open questions remaining as well, some of which are discussed in this proposal. New research topics include the connection between IP and machine learning, IP for nonlinear equations, IP for nonlocal operators, and connections between statistics and IP.
Updated on Jul 10, 2025 09:26 AM PDT -
Program Geometric Measure Theory
Organizers: Otis Chodosh (Stanford University), Camillo De Lellis (Institute for Advanced Study), LEAD Guido De Philippis (Hausdorff Research Institute for Mathematics, University of Bonn), Svitlana Mayboroda (University of Minnesota, Twin Cities), Robin Neumayer (Northwestern University), Luca Spolaor (University of California, San Diego), Zihui Zhao (Johns Hopkins University)The field of Geoemtric Measure Theory (GMT)has become vast and many gaps between disparate areas have emerged. This thematic semester will bring together researchers from every corner of the field, to kick-start new interactions and discoveries. In light of the many exciting advancements and potential for future breakthroughs, this as a crucial moment to bring old and new members of the GMT community together. The program will encourage interactions between established experts, emerging researchers and students, allowing for the sharing of key idea that brought to the recent developments and helping to shape a research agenda for the future.
Updated on Jul 10, 2025 09:27 AM PDT
Past Scientific Events
-
Seminar ADJOINT/MSRI-UP panel
Created on May 13, 2025 11:33 AM PDT -
Summer Graduate School Computer Assisted Proofs in Applied Mathematics (SLMath)
Organizers: LEAD Jonathan Jaquette (New Jersey Institute of Technology), Evelyn Sander (George Mason University)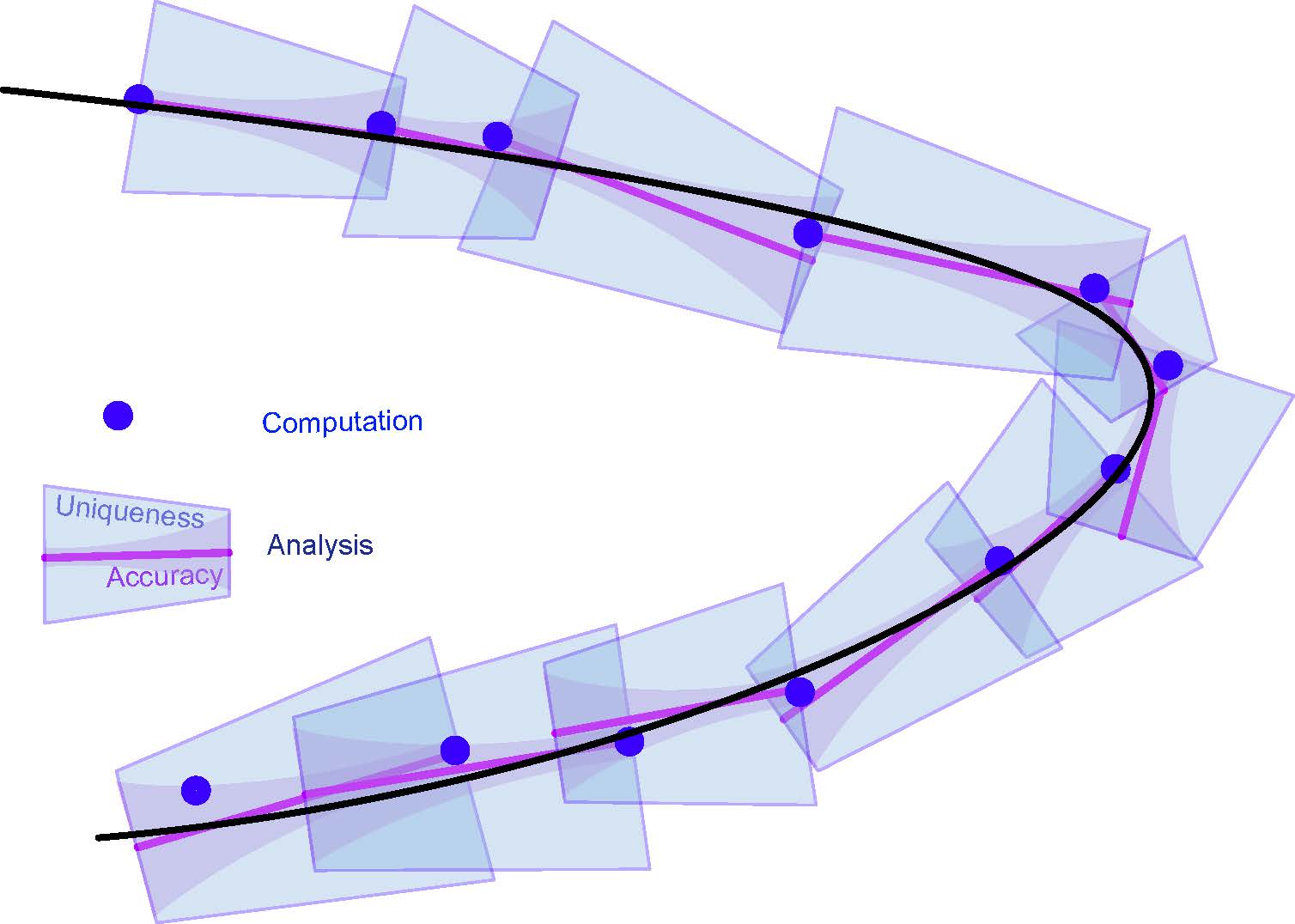
One of the core elements of applied mathematics is mathematical modeling consisting of nonlinear equations such as ODEs, and PDEs. A fundamental difficulty which arises is that most nonlinear models cannot be solved in closed form. Computer assisted proofs are at the forefront of modern mathematics and have led to many important recent mathematical advances. They provide a way of melding analytical techniques with numerical methods, in order to provide rigorous statements for mathematical models that could not be treated by either method alone. In this summer school, students will review standard computational and analytical techniques, learn to combine these techniques with more specialized methods of interval arithmetic, and apply these methods to establish rigorous results in otherwise intractable problems
Updated on Jul 10, 2025 03:29 PM PDT -
Summer Graduate School Principled Scientific Discovery with Formal Methods (IBM, Yorktown)
Organizers: Kenneth Clarkson (IBM Research Division), Cristina Cornelio (Samsung AI), Claudia D Ambrosio (Centre National de la Recherche Scientifique (CNRS); École Polytechnique), Sanjeeb Dash (IBM Thomas J. Watson Research Center), Lior Horesh (IBM Thomas J. Watson Research Center) <p>The traditional scientific method cycle, with Francis Bacon and Rene Descartes, its concievers in the center, alongside formal and statistical AI machinary, as a propsective evolution of the method. <br /> </p>
<p>The traditional scientific method cycle, with Francis Bacon and Rene Descartes, its concievers in the center, alongside formal and statistical AI machinary, as a propsective evolution of the method. <br /> </p>The summer school aims to expose participants to formal methods that can facilitate principled scientific discovery. The school will cover some of the basic automated statistical inference (in the form of machine learning techniques) and reasoning methods that are commonly used in scientific discovery, as well as novel techniques developed to tackle open questions and issues. This summer school will address novel computational methods for scientific discovery and focus on fusing axiomatic knowledge and experimental data to enable principled derivations of models of natural phenomena along with certificates of the consistency of these models with background knowledge specified as axioms.
Updated on May 23, 2025 08:55 AM PDT -
African Diaspora Joint Mathematics ADJOINT 2025
ADJOINT is a yearlong program that provides opportunities for U.S. mathematicians to conduct collaborative research on topics at the forefront of mathematical and statistical research. Participants will spend two weeks taking part in an intensive collaborative summer session at SLMath. The two-week summer session for ADJOINT 2025 will take place June 30 - July 11, 2025 in Berkeley, California. Researchers can participate in either of the following ways: (1) joining ADJOINT small groups under the guidance of some of the nation's foremost mathematicians and statisticians to expand their research portfolio into new areas, or (2) applying to Self-ADJOINT as part of an existing or newly-formed independent research group ((three-to-five participants is preferred) to work on a new or established research project. Throughout the following academic year, the program provides conference and travel support to increase opportunities for collaboration, maximize researcher visibility, and engender a sense of community among participants.
Updated on Jun 06, 2025 10:11 AM PDT -
Summer Graduate School Noncommutative Algebraic Geometry (Antwerp, Belgium)
Organizers: Pieter Belmans (University of Luxembourg), Lander Hermans (Universiteit Antwerp), Wendy Lowen (Universiteit Antwerpen), Arne Mertens (Universiteit Antwerp), Michel VAN DEN BERGH (Hasselt University), Špela Špenko (Université Libre de Bruxelles)
The school will consist of two courses: Homological Mirror Symmetry and Algebraic Models for Spaces. These courses will be planned and taught by organisers with the help of teaching assistants for the problem sessions. The school will be aimed at a wide range of graduate students, from students with a Bachelor degree to beginning PhD students. The lectures and problem sessions will be complemented by a poster session in week one and a total of four introductory research talks on Friday afternoons.
Updated on May 22, 2025 10:57 AM PDT -
Summer Graduate School Graphical Models in Algebraic Combinatorics (SLMath)
Organizers: Christian Gaetz (University of California, Berkeley), David Keating (University of Illinois at Urbana-Champaign), Melissa Sherman-Bennett (University of California, Davis), LEAD Anna Weigandt (University of Minnesota)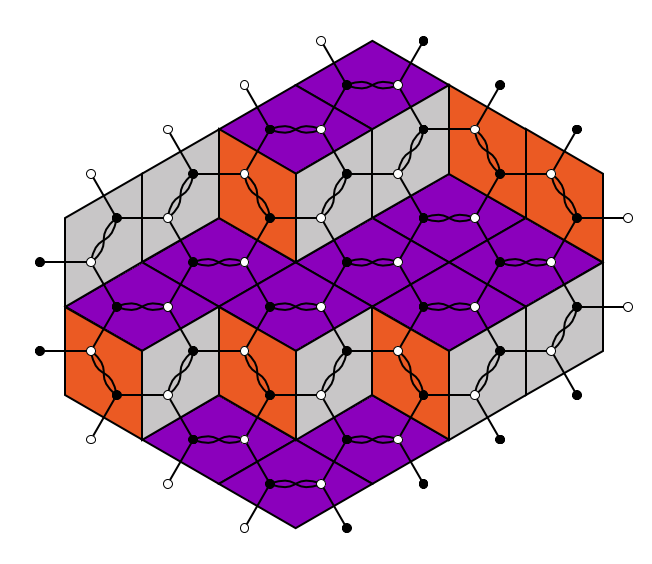 <p>A plane partition and an hourglass plabic graph</p>
<p>A plane partition and an hourglass plabic graph</p>This school will introduce students to a range of powerful combinatorial tools used to understand algebraic objects ranging from the homogeneous coordinate ring of the Grassmannian to symmetric functions. The summer school will center around two main lecture series "Webs and Plabic Graphs" and "Vertex Models and Applications". While the exact applications differ, both courses will center on graphical models for algebraic problems closely related to Grassmannian and its generalizations. This school will be accessible to a wide range of students. Students will leave the school with a solid grasp of the combinatorics of webs, plabic graphs, and the six-vertex model, an understanding of their algebraic applications, and a taste of current research directions.
Updated on Jul 02, 2025 10:42 AM PDT -
Summer Graduate School New Perspectives on Discriminants and Applications (Leipzig, Germany)
Organizers: Eliana Duarte (Centro de Matemática da Universidade do Porto), Serkan Hosten (San Francisco State University), Simon Telen (Max-Planck-Institut)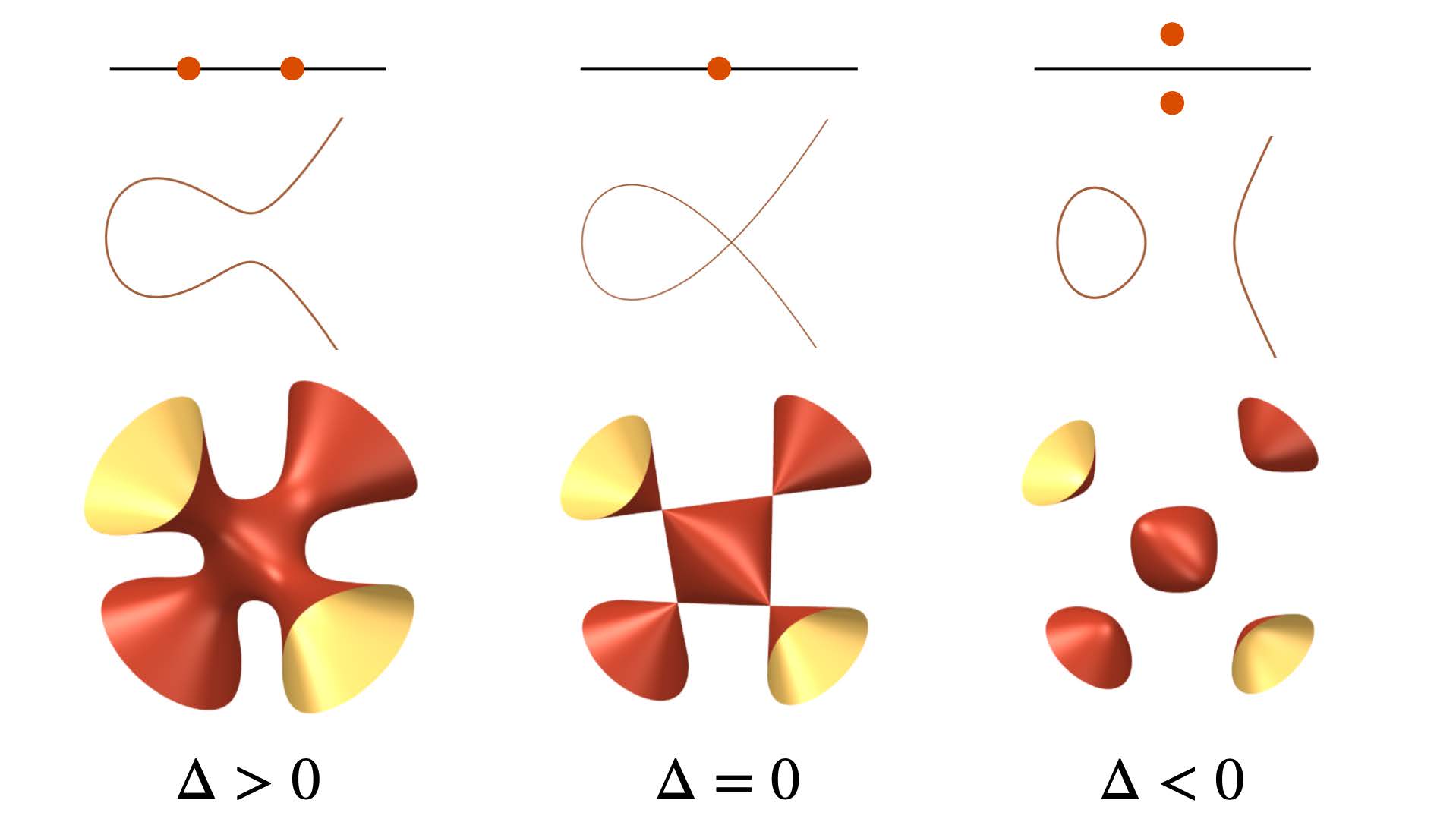 <p>The discriminant ∆ detects singular varieties. The picture shows three different scenarios: solutions of quadratic polynomials, cubic plane curves and cubic surfaces.</p>
<p>The discriminant ∆ detects singular varieties. The picture shows three different scenarios: solutions of quadratic polynomials, cubic plane curves and cubic surfaces.</p>This summer school will offer a hands-on introduction to discriminants, with a view towards modern applications. Starting from the basics of computational algebraic geometry and toric geometry, the school will gently introduce participants to the foundations of discriminants. A particular emphasis will be put on computing discriminants of polynomial systems using computer algebra software. Then, we will dive into three applications of discriminants: algebraic statistics, geometric modeling, and particle physics. Here, discriminants contribute to the study of maximum likelihood estimation, to finding practical parametrizations of geometric objects, and to computations of scattering amplitudes. We will explain recently discovered unexpected connections between these three applications. In addition to lectures, the summer school will have daily collaborative exercise sessions which will be guided by the teaching assistants and will include software demonstrations.
Updated on Jul 03, 2025 09:26 AM PDT -
Summer Graduate School Mathematics of Sea Ice and Polar Ecosystems (Fairbanks, Alaska)
Organizers: Kenneth Golden (University of Utah), Jody Reimer (University of Utah) From micro to macro, sea ice supports life in the polar regions. Left: illustration of the porous sea ice microstructure, home to a microbial community of ice endemic organisms including bacteria and algae. Right: two penguins on Antarctic sea ice.
From micro to macro, sea ice supports life in the polar regions. Left: illustration of the porous sea ice microstructure, home to a microbial community of ice endemic organisms including bacteria and algae. Right: two penguins on Antarctic sea ice.In this summer school, students will be introduced to mathematical and computational modeling of sea ice and polar ecosystems. As a material, sea ice is a multiscale composite structured on length scales ranging from tenths of millimeters to tens of kilometers. From tiny brine inclusions and surface melt ponds of increasing complexity, to ice floes of varying sizes in a seawater host, a principal challenge is how to find sea ice effective properties that are relevant to larger scale models, given data on smaller scale structures. Similarly, the sea ice ecosystem ranges from algae living in the brine inclusions to charismatic megafauna like penguins and polar bears, whose diets depend critically, down the line, on the tiny sea ice extremophiles. The dynamics of sea ice microbial communities are regulated by the physics of the ice microstructure, and, in turn, many of these microbes modify their environment by secreting extracellular polymeric substances. In addition to sea ice and its ecosystems, we will consider broader mathematical models including energy balance models, tipping points, and global circulation models.
Updated on Jun 10, 2025 09:42 AM PDT -
Summer Graduate School Statistical Optimal Transport (SLMath)
Organizers: LEAD Promit Ghosal (University of Chicago), Jonathan Niles Weed (New York University, Courant Institute), Marcel Nutz (Columbia University)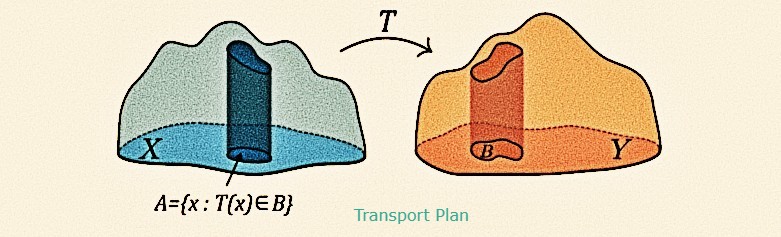
This summer school offers an exceptional opportunity for participants to delve into the intricate realm of statistical optimal transport theory. This captivating field stands at the crossroads of multiple disciplines, drawing from a rich tapestry of mathematical insights from diverse subjects, including partial differential equations, stochastic analysis, convex geometry, statistics, and machine learning, crafting a vibrant and interdisciplinary landscape. The foremost objective of this summer school is to create a dynamic learning environment that unites students from diverse backgrounds such as PDE theory, probability, or optimal transport.
Updated on Jun 12, 2025 11:26 AM PDT -
Summer Graduate School Local Limits of Random Graphs (Paris-Saclay University, France)
Organizers: Ainhoa Aparicio-Monforte (Fondation Mathématique Jacques Hadamard (FMJH)), Alexandra Genesco (Fondation Mathématique Jacques Hadamard (FMJH)), LEAD Pascal Massart (Fondation Mathématique Jacques Hadamard (FMJH)) <p>A display of the evolution of an Erdos-Renyi random graph . </p>
<p>A display of the evolution of an Erdos-Renyi random graph . </p>Random graphs are ubiquitous in modern probability theory. Besides their intrinsic mathematical beauty, they are also used to model complex networks. In the early 2000’s, I. Benjamini and O. Schramm introduced a mathematical framework in which they endowed the set of locally finite rooted connected graphs with the structure of a Polish space, called the local topology. The goal of this summer school is to introduce the framework of local limits of random graphs, the concepts of Benjamini-Schramm (or unbiased) limits and unimodularity, as well as the most important applications. The lectures will be delivered by Nicolas Curien (Prof. Paris-Saclay University) and Justin Salez (Prof. Université Paris-Dauphine) and will be complemented by many problem sessions, where students will work in small groups under the guidance of teaching assistants, who are researchers in the field.
Updated on Jun 06, 2025 09:24 AM PDT -
Summer Graduate School 2025 PIMS-CRM Summer School in Probability (Vancouver, Canada)
Organizers: Louigi Addario-Berry (McGill University), Omer Angel (University of British Columbia), Mathav Murugan (University of British Columbia), Gordon Slade (University of British Columbia)The Summer Schools in Probability are a highlight of Canadian probability and are internationally significant. Launched by PIMS in 2004, the school takes the form of two main 4-week courses along with three mini-courses. The schools have played a major role in the development of an exceptionally strong community of young probabilist in Canada, North America and overseas. This will be the 13th time this school has run.
Updated on Jul 01, 2025 11:35 AM PDT -
Summer Graduate School Séminaire de Mathématiques Supérieures 2025: An Introduction to Recent Trends in Commutative Algebra (Toronto, Canada)
Organizers: Sergio Da Silva (Virginia State University), Federico Galetto (Cleveland State University), Elena Guardo (Università di Catania), Megumi Harada (McMaster University), Patricia Klein (Texas A & M University), Jenna Rajchgot (McMaster University), Adam Van Tuyl (McMaster University)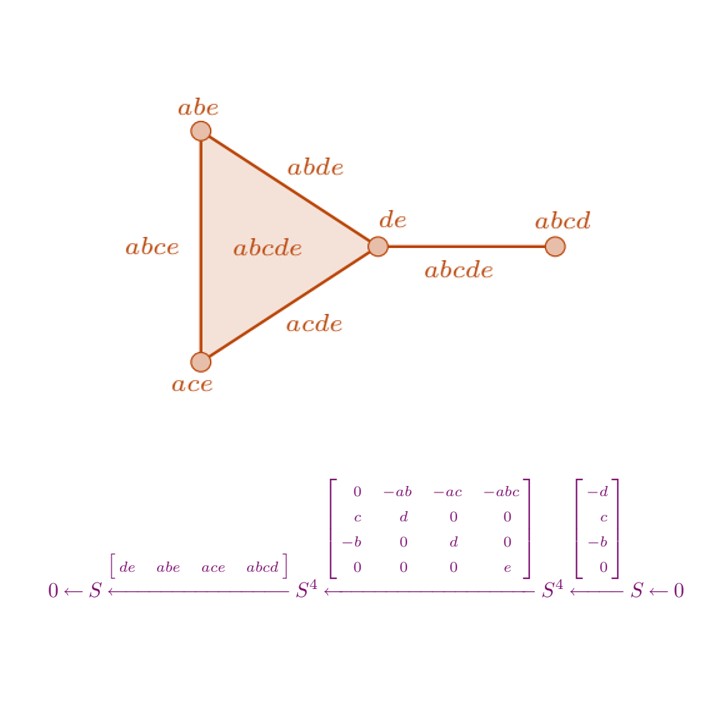 <p>A minimal free resolution supported on a simplicial complex</p>
<p>A minimal free resolution supported on a simplicial complex</p>The 2025 SMS will allow graduate students to learn about a number of recent trends and advances in the field of commutative algebra. The aim of the SMS is to provide an “on-ramp” for graduate students interested in algebra, combinatorics, and/or algebraic combinatorics to learn more about commutative algebra’s interaction with these fields. The introductory courses will introduce fundamental skills in commutative algebra, the more intermediate courses will expose students to cutting-edge research in the field. The school will focus on four topics within commutative algebra: Combinatorial Methods, Homological Methods, Computational Methods, and Characteristic p Methods. The SMS will provide both a series of introductory lectures and intermediate/advanced lectures from leaders in one of the four areas. The lectures will include a series of problem sessions that will allow participants to develop and hone their skills in these areas, which will be especially helpful for new people to the field. Participants will be encouraged to work collaboratively, both to enhance their own mathematical networks as well as to promote future collaborations beyond the school.
Updated on Feb 19, 2025 04:14 PM PST -
Seminar PSDS Seminar: Playing Sudoku on random 3-regular graphs
Updated on May 12, 2025 08:02 AM PDT -
Seminar PSDS Open Problem Session
Updated on Feb 28, 2025 08:01 AM PST -
Seminar EC Seminar: Asymptotic Gyarfas Sumner
Updated on May 06, 2025 01:55 PM PDT -
Seminar EC Seminar: Graph decompositions in random settings via refined absorption
Updated on May 08, 2025 09:11 AM PDT -
Seminar PSDS & EC Joint Seminar: Random Ramsey, homology, and high-dimensional phase transitions in random graphs
Updated on May 09, 2025 08:04 AM PDT -
Seminar Talent Show
Updated on Apr 29, 2025 01:57 PM PDT -
Seminar PSDS Open Problem Session
Updated on Feb 28, 2025 08:01 AM PST -
Seminar Graduate Student Seminar Series: Lattice packing of spheres in high dimensions using a stochastically evolving ellipsoid
Updated on May 02, 2025 12:36 PM PDT -
Seminar PSDS Seminar: Planted clique recovery in geometric graphs
Updated on May 05, 2025 11:11 AM PDT -
Seminar Professional Development Seminar: Careers in Industry
Updated on May 02, 2025 11:30 AM PDT -
Seminar Panelist Lunch
Updated on May 02, 2025 11:10 AM PDT -
Seminar EC Seminar: Erdős–Pósa of cycles that are far apart
Updated on May 01, 2025 02:31 PM PDT -
Seminar EC Seminar: Ramsey with purple edges
Updated on May 01, 2025 02:37 PM PDT -
Seminar PSDS & EC Joint Seminar: Counting score sequences (and graphic sequences) via random walks
Updated on Apr 30, 2025 12:57 PM PDT